Question

【题目】八年级的小明同学通到这样一道数学题目：△ABC为边长为4的等边三角形，E是边AB边上任意一动点，点D在CB的延长线上，且满足AE＝BD．

（1）如图①，当点E为AB的中点时，DE＝　 　；

（2）如图②，点E在运动过程中，DE与EC满足什么数量关系？请说明理由；

（3）如图③，F是AC的中点，连接EF．在AB边上是否存在点E，使得DE+EF值最小？若存在，求出这个最小值；若不存在，请说明理由．（直角三角形中，30°所对的边是斜边的一半）

Answer 1

【答案】（1）2；（2）DE＝CE，理由见解析；（3）这个最小值为2；

【解析】

（1）如图①，过点E作EH⊥BC于H，由等边三角形的性质可得BE=DB=AE=2，由直角三角形的性质可求BH=1，EH，由勾股定理可求解；

（2）如图②，过E作EF∥BC交AC于F，可证△AEF是等边三角形，AE=EF=AF=BD，由“SAS”可证△DBE≌△EFC，可得DE=CE；

（3）如图③，将△ABC沿AB翻折得到△ABC'，连接C'F交AB于点E'，连接CE'，DE'，过点F作FH⊥AC'于点H，由“SAS”可证△ACE'≌△AC'E'，可得C'E'=CE'，可得当点C'，点E'，点F三点共线时，DE+EF的值最小，由勾股定理可求最小值.

（1）如图①，过点E作EH⊥BC于H，

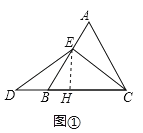
∵△ABC为边长为4的等边三角形，点E是AB的中点，

∴AE=BE=2=DB，∠ABC=60°，且EH⊥BC，

∴∠BEH=30°，

∴BH=1，EHBH，

∴DH=DB+BH=2+1=3，

∴DE.

故答案为：；

（2）DE=CE.理由如下：

如图②，过E作EF∥BC交AC于F.

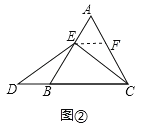
∵△ABC是等边三角形，

∴∠ABC=∠ACB=∠A=60°，AB=AC=BC.

∵EF∥BC，

∴∠AEF=∠ABC=60°，∠AFE=∠ACB=60°，

∴∠AEF=∠AFE=∠A=60°，

∴△AEF是等边三角形，

∴AE=EF=AF，

∴AB﹣AE=AC﹣AF，

∴BE=CF.

∵∠ABC=∠ACB=∠AFE=60°，

∴∠DBE=∠EFC=120°，且AE=EF=DB，BE=CF，

∴△DBE≌△EFC(SAS)，

∴DE=CE，

（3）如图③，将△ABC沿AB翻折得到△ABC'，连接C'F交AB于点E'，连接CE'，DE'，过点F作FH⊥AC'于点H.

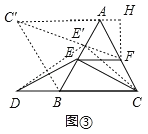
∵将△ABC沿AB翻折得到△ABC'，

∴AC=AC'=BC=BC'=4，∠BAC=∠BAC'=60°，且AE'=AE'，

∴△ACE'≌△AC'E'(SAS)，

∴C'E'=CE'，

由（2）可知：DE'=CE'，

∴C'E'=CE'=DE'.

∵DE+EF=C'E+EF=C'E'+EF，

∴当点C'，点E'，点F三点共线时，DE+EF的值最小.

∵F是AC的中点，

∴AF=CF=2，且HF⊥AC'，∠FAH=180°﹣∠CAB﹣∠C'AB=60°，

∴AH=1，HFAH，

∴C'H=4+1=5，

∴C'F，

∴DE+EF的最小值为.