Question

（本题满分10分）（1）探究新知：

①如图，已知AD∥BC，AD＝BC，点M，N是直线CD上任意两点．试判断△ABM与△ABN的面积是否相等。 

②如图，已知AD∥BE，AD＝BE，AB∥CD∥EF，点M是直线CD上任一点，点G是直线EF上任一点．试判断△ABM与△ABG的面积是否相等，并说明理由．  

 

 

 

 

 

 

 

 

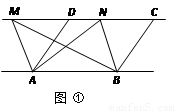
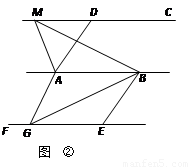
（2）结论应用：    

如图③，抛物线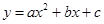的顶点为C（1，4），交x轴于点A（3，0），交y轴于点D．试探究在抛物线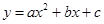上是否存在除点C以外的点E，使得△ADE与△ACD的面积相等？ 若存在，请求出此时点E的坐标，若不存在，请说明理由．

    

 

Answer 1

【答案】

 

解：﹙1﹚相等       ---------------------1分

 

②相等．理由如下：分别过点D，E作DH⊥AB，EK⊥AB，垂足分别为H，K．

则∠DHA＝∠EKB＝90°．∵ AD∥BE，∴ ∠DAH＝∠EBK．∵ AD＝BE，

∴ △DAH≌△EBK．  ∴ DH＝EK． ∵ CD∥AB∥EF，   

∴S_△ABM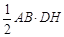＝，S_△ABG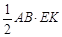＝，  ∴  S_△ABM＝ S_△ABG. -------------4分

﹙2﹚答：存在．---------------------5分

解：因为抛物线的顶点坐标是C(1，4)，所以，可设抛物线的表达式为.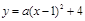

又因为抛物线经过点A(3，0)，将其坐标代入上式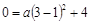，得，解得.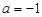

∴ 该抛物线的表达式为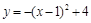，即．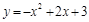

∴ D点坐标为（0，3）．

设直线AD的表达式为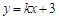，代入点A的坐标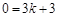，得，解得.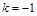

∴ 直线AD的表达式为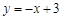．   ---------------------7分

过C点作CG⊥x轴，垂足为G，交AD于点H．则H点的纵坐标为．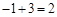

∴ CH＝CG－HG＝4－2＝2．

设点E的横坐标为m，则点E的纵坐标为．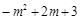   

过E点作EF⊥x轴，垂足为F，交AD于点P，则点P的纵坐标为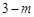，EF∥CG．

由﹙1﹚可知：若EP＝CH，则△ADE与△ADC的面积相等．

 

 

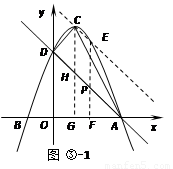
①若E点在直线AD的上方﹙如图③-1﹚，

则P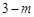F＝，EF＝．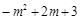

∴ EP＝EF－PF＝＝．∴ ．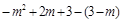 

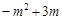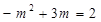解得，．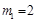

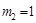当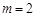时，PF＝3－2＝1，EF＝1+2＝3．  ∴ E点坐标为（2，3）．  

同理 当m＝1时，E点坐标为（1，4），与C点重合． 

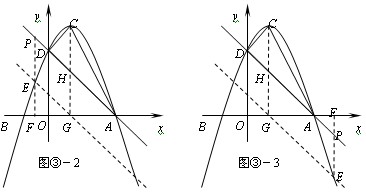
②若E点在直线AD的下方﹙如图③－2,③－3﹚，

则．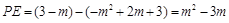

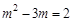∴．解得，．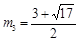 

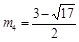当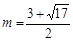时，E点的纵坐标为；   

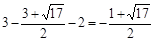当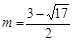时，E点的纵坐标为．  

∴ 在抛物线上存在除点C以外的点E，使得△ADE与△ACD的面积相等，E点的坐标为E₁（2，3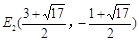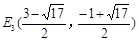）；；．--------------10分

【解析】

此题有较强的综合性，难度较大。代数与几何兼有，既有几何中的三角形全等、平行线的性质，又有代数中的二次函数。