练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．如图，已知AC与BC相交于点O，∠C=∠D=75°，∠A=35°，则∠B的度数为（　　）
    A．25°B．35°C．40°D．45°

    分析 根据三角形的内角和定理求出∠AOD，根据对顶角相等可得∠BOC=∠AOD，再根据三角形的内角和等于180°列式计算即可得解．

    解答 解：在△AOD中，∵∠D=75°，∠A=35°，
    ∴∠AOD=180°-∠A-∠D=180°-35°-75°=70°，
    ∵∠BOC=∠AOD=70°（对顶角相等），
    ∴在△BOC中，∠B=180°-∠BOC-∠C=180°-70°-75°=35°．
    故选B．

    点评 本题考查了三角形的内角和定理，对顶角相等的性质，熟记定理并准确识图理清图中各角度之间的关系是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    11．如图，在平面直角坐标系中，抛物线y=ax2+bx+6经过点A（-3，0）和点B（2，0），直线y=h（h为常数，且0＜h＜6）与BC交于点D，与y轴交于点E，与AC交于点F．
    （1）求抛物线的解析式；
    （2）连接AE，求h为何值时，△AEF的面积最大．
    （3）已知一定点M（-2，0），问：是否存在这样的直线y=h，使△BDM是等腰三角形？若存在，请求出h的值和点D的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，河岸边有座塔AB，小敏在河对岸C处测得塔顶A的仰角为30°，向塔前进20米到达D处，又测得塔顶A的仰角为45°，请根据上述数据计算水塔的高．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．古希腊的毕达哥拉斯学派由古希腊哲学家毕达哥斯拉所创立，毕达哥斯拉学派认为数是万物的本原，事物的性质是由某市数量关系决定的，如他们研究各种多边形数：
    记第n个k边形数N（n，k）=$\frac{k-2}{2}$n2+$\frac{4-k}{2}$n（m≥1，k≥3，k，n都为整数）
    如第1个三角形数N（1，3）=$\frac{3-2}{2}$×12+$\frac{4-3}{2}$×1=1；
    第2个三角形数N（2，3）=$\frac{3-2}{2}$×22+$\frac{4-3}{2}$×2=3；
    第3个三角形数N（3，4）=$\frac{4-2}{2}$×32+$\frac{4-4}{2}$×3=9；
    第4个三角形数N（4，4）=$\frac{4-2}{2}$×42+$\frac{4-4}{2}$×4=16
    （1）N（5，3）=15，N（6，5）=51；
    （2）若N（m，6）比N（m+2，4）大10，求m的值；
    （3）若记y=N（6，t）-N（t，5），试求出y的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

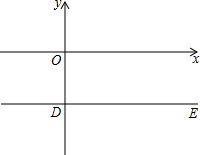    2．已知：直线l：y=2x+2b与过点D（0，-2）平行于x轴的直线DE交于B点，与x轴交于点A．
    （1）求A、B两点的坐标；（用含b的代数式表示）；
    （2）当△ABD是以AD为底边的等腰三角形时，求b的值；
    （3）设直线y=2x+2b与y轴交于点C，当△CAO的面积是△CBD的面积的4倍时，求b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知：如图，四边形ABCD中，∠A=∠C=90°，∠D=60°，AD=5$\sqrt{3}$，AB=3，求BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图，三角形ABC中，AB=AC=2，∠B=15°，求AB边上的高．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．设A=-$\frac{1}{2}$x-4（x-$\frac{1}{3}$y）+（-$\frac{3}{2}$x+$\frac{2}{3}$y）．
    （1）当x=-$\frac{1}{3}$，y=1时，求A的值；
    （2）若使求得的A的值与（1）中的结果相同，则给出的x、y的条件还可以是-3x+y=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

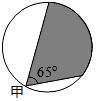    17．如图，是一个圆形展厅，为了监控整个展厅，在其圆形边缘上安装了甲、乙两台监视器，若甲监视器的监控角度为65°，则乙监控器的监控角度至少为（　　）
    A．25°B．65°C．115°D．130°

    查看答案和解析>>

    同步练习册答案