
 , 则
, 则 ( )
( ) A. | B.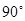 | C. | D. |

科目:初中数学 来源:不详 题型:解答题
 同侧,在直线
同侧,在直线 上找一点P,使AP+BP的值最小.
上找一点P,使AP+BP的值最小. 的对称点
的对称点 ,连接
,连接 ,与直线
,与直线 的交点就是所求的点P
的交点就是所求的点P


查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ),使得AC+CD+DB最短.(不要求写画法)
),使得AC+CD+DB最短.(不要求写画法)
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 在平面直角坐标系中的位置如下图所示.
在平面直角坐标系中的位置如下图所示.
 的坐标;
的坐标; 绕点
绕点 按逆时针方向旋转
按逆时针方向旋转 后的
后的 ;
; 旋转到点
旋转到点 所经过的路线长(结果保留
所经过的路线长(结果保留 ).
).查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的位置如图所示
的位置如图所示 绕点
绕点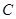 顺时针方向旋转
顺时针方向旋转 后得
后得
 点的对应点
点的对应点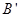 的坐标;
的坐标; 点旋转到点
点旋转到点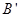 所经过的路线长(结果保留
所经过的路线长(结果保留 )
)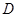 ,并画出以
,并画出以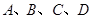 为顶点的四边形,使其为中心对称图形(画一个即可)。
为顶点的四边形,使其为中心对称图形(画一个即可)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com