
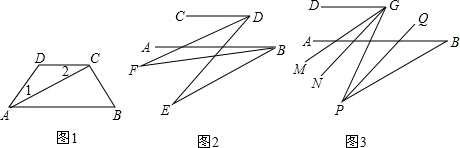
分析 (1)根据内错角相等,两直线平行证明即可;
(2)先由角平分线的定义可得:$∠CDF=\frac{1}{2}∠CDE$=35°,∠ABE=2∠ABF,然后根据两直线平行内错角相等,可得:∠2=∠CDF=35°,然后利用三角形外角的性质求出∠ABF的度数,进而可求∠ABE的度数;
(3)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠1=∠BPG+∠B,再根据平行线的性质以及角平分线的定义表示出∠MGP、∠DPQ,根据两直线平行,内错角相等可得∠NGP=∠GPQ,然后列式表示出∠MGN=$\frac{1}{2}$∠B,从而判定②正确.
解答 (1)答:AB∥CD.
证明:∵AC平分∠DAB,
∴∠1=∠CAB,
∵∠1=∠2,
∴∠2=∠CAB,
∴AB∥CD;
(2)解:如图2,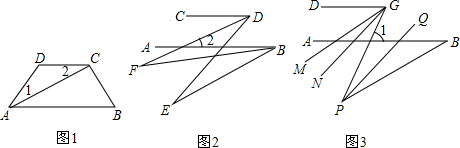
∵BF平分∠ABE,DF平分∠CDE,
∴$∠CDF=\frac{1}{2}∠CDE$=35°,∠ABE=2∠ABF,
∵CD∥AB,
∴∠2=∠CDF=35°,
∵∠2=∠DFB+∠ABF,∠DFB=20°,
∴∠ABF=15°,
∴∠ABE=2∠ABF=30°;
(3)解:如图3,根据三角形的外角性质,∠1=∠BPG+∠B,
∵PQ平分∠BPG,GM平分∠DGP,
∴∠GPQ=$\frac{1}{2}$∠BPG,∠MGP=$\frac{1}{2}$∠DGP,
∵AB∥CD,
∴∠1=∠DGP,
∴∠MGP=$\frac{1}{2}$(∠BPG+∠B),
∵PQ∥GN,
∴∠NGP=∠GPQ=$\frac{1}{2}$∠BPG,
∴∠MGN=∠MGP-∠NGP=$\frac{1}{2}$(∠BPG+∠B)-$\frac{1}{2}$∠BPG=$\frac{1}{2}$∠B,
根据前面的条件,∠B=30°,
∴∠MGN=$\frac{1}{2}$×30°=15°,
∴①∠DGP-∠MGN的值随∠DGP的变化而变化;②∠MGN的度数为15°不变.
点评 本题考查了平行线的判定与性质,三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,综合性较强,难度较大,仔细分析图形,理清各角度之间的关系是解题的关键,也是本题的难点.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
 如图,在一次夏令营活动中,小明从营地A到C地去,先沿北偏东70°方向到达B地,再沿北偏西20°方向到达C地,此时∠ACB=60°,问小明在营地A的( )
如图,在一次夏令营活动中,小明从营地A到C地去,先沿北偏东70°方向到达B地,再沿北偏西20°方向到达C地,此时∠ACB=60°,问小明在营地A的( )| A. | 北偏东20°方向上 | B. | 北偏东30°方向上 | C. | 北偏西30°方向上 | D. | 北偏东40°方向上 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F,那么EC与DF平行吗?为什么?请完成下面的解题过程.
如图:∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F,那么EC与DF平行吗?为什么?请完成下面的解题过程.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两组对边相等的四边形 | |
| B. | 两组对角相等的四边形 | |
| C. | 一组对边平行,一组邻角互补的四边形 | |
| D. | 一组对边平行,一组对角相等的四边形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,∠1=∠2,DE⊥BC,AB⊥BC,那么∠A=∠3吗?说明理由.(请为每一步推理注明依据)
如图,∠1=∠2,DE⊥BC,AB⊥BC,那么∠A=∠3吗?说明理由.(请为每一步推理注明依据) 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,若点A(-2,n),B(1,-2)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,在平面直角坐标系xOy中,若点A(-2,n),B(1,-2)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com