
【题目】如图,△ABC内接于⊙O,CA=CB,CD∥AB且与OA的延长线交与点D.
(1)判断CD与⊙O的位置关系并说明理由;
(2)若∠ACB=120°,OA=2,求CD的长.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根![]() .
.
(1)求实数k的取值范围.
(2)若方程两实根![]() 满足|x1|+|x2|=x1·x2,求k的值.
满足|x1|+|x2|=x1·x2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 随机抛掷一枚均匀的硬币,落地后反面一定朝上。
B. 从1,2,3,4,5中随机取一个数,取得奇数的可能性较大。
C. 某彩票中奖率为![]() ,说明买100张彩票,有36张中奖。
,说明买100张彩票,有36张中奖。
D. 打开电视,中央一套正在播放新闻联播。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 xOy 中,直线 y ![]() x 4与 x 轴、y 轴分别交于点 A、点 B,点 D 在 y 轴的负半轴上,若将△DAB 沿着直线 AD 折叠,点 B 恰好落在 x 轴正半轴上的点 C处.
x 4与 x 轴、y 轴分别交于点 A、点 B,点 D 在 y 轴的负半轴上,若将△DAB 沿着直线 AD 折叠,点 B 恰好落在 x 轴正半轴上的点 C处.
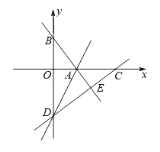
(1)求直线 CD 的表达式;
(2)在直线 AB 上是否存在一点 P,使得 SPCD![]() SOCD?若存在,直接写出点 P 的坐标;若不存在,请说明理由.
SOCD?若存在,直接写出点 P 的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为( )

A. 140° B. 100° C. 50° D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O恰好经过边BC的中点D,并与边AC相交于另一点F.

(1)求证:BD是⊙O的切线.
(2)若AB=![]() ,E是半圆
,E是半圆![]() 上一动点,连接AE,AD,DE.
上一动点,连接AE,AD,DE.
填空:
①当![]() 的长度是____________时,四边形ABDE是菱形;
的长度是____________时,四边形ABDE是菱形;
②当![]() 的长度是____________时,△ADE是直角三角形.
的长度是____________时,△ADE是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数![]() 反比例函数
反比例函数![]() 由
由![]() 构造一个新函数
构造一个新函数![]() 其图象如图所示.(因其图象似双钩,我们称之为“双钩函数” ).给出下列几个命题:
其图象如图所示.(因其图象似双钩,我们称之为“双钩函数” ).给出下列几个命题:

①该函数的图象是中心对称图形;
②当![]() 时,该函数在
时,该函数在![]() 时取得最大值-2;
时取得最大值-2;
③![]() 的值不可能为1;
的值不可能为1;
④在每个象限内,函数值![]() 随自变量
随自变量![]() 的增大而增大.
的增大而增大.
其中正确的命题是 .(请写出所有正确的命题的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强的钱包内有10元钱、20元钱和50元钱的纸币各1张.
(1)若从中随机取出1张纸币,求取出纸币的金额是20元的概率;
(2)若从中随机取出2张纸币,求取出纸币的总额可购买一件51元的商品的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com