
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于E.
(1)如图1,连接CE,求证:△BCE是等边三角形;
(2)如图2,点M为CE上一点,连结BM,作等边△BMN,连接EN,求证:EN∥BC;
(3)如图3,点P为线段AD上一点,连结BP,作∠BPQ=60°,PQ交DE延长线于Q,探究线段PD,DQ与AD之间的数量关系,并证明.

【答案】(1)见解析;(2)见解析;(3)DQ=AD+DP.
【解析】
(1)由直角三角形的性质得出∠ABC=60°,由角平分线的定义得出∠A=∠DBA,证出AD=BD,由线段垂直平分线的性质得出AE=BE,由直角三角形斜边上的中线性质得出CE=![]() AB=BE,即可得出结论;
AB=BE,即可得出结论;
(2)由等边三角形的性质得出BC=BE,BM=BN,∠EBC=∠MBN=60°,证出∠CBM=∠EBN,由SAS证明△CBM≌△EBN,得出∠BEN=∠BCM=60°,得出∠BEN=∠EBC,即可得出结论;
(3)延长BD至F,使DF=PD,连接PF,证出△PDF为等边三角形,得出PF=PD=DF,∠F=∠PDQ=60°,得到∠F=∠PDQ=60°,证出∠Q=∠PBF,由AAS证明△PFB≌△PDQ,得出DQ=BF=BD+DF=BD+DP,证出AD=BD,即可得出结论.
(1)证明:∵∠ACB=90°,∠A=30°,
∴∠ABC=60°,
∵BD是△ABC的角平分线,
∴∠DBA=![]() ∠ABC=30°,
∠ABC=30°,
∴∠A=∠DBA,
∴AD=BD,
∵DE⊥AB,
∴AE=BE,
∴CE=![]() AB=BE,
AB=BE,
∴△BCE是等边三角形;
(2)证明:∵△BCE与△MNB都是等边三角形,
∴BC=BE,BM=BN,∠EBC=∠MBN=60°,
∴∠CBM=∠EBN,
在△CBM和△EBN中,

∴△CBM≌△EBN(SAS),
∴∠BEN=∠BCM=60°,
∴∠BEN=∠EBC,
∴EN∥BC;
(3)解:DQ=AD+DP;理由如下:
延长BD至F,使DF=PD,连接PF,如图所示:
∵∠PDF=∠BDC=∠A+∠DBA=30°+30°=60°,
∴△PDF为等边三角形,
∴PF=PD=DF,∠F=60°,
∵∠PDQ=90°-∠A=60°,
∴∠F=∠PDQ=60°,
∴∠BDQ=180°-∠BDC-∠PDQ=60°,
∴∠BPQ=∠BDQ=60°,
∴∠Q=∠PBF,
在△PFB和△PDQ中,

∴△PFB≌△PDQ,
∴DQ=BF=BD+DF=BD+DP,
∵∠A=∠ABD,
∴AD=BD,
∴DQ=AD+DP.


科目:初中数学 来源: 题型:
【题目】如图,直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知顶点为![]() 的抛物线
的抛物线![]() 经过点
经过点![]() ,点
,点![]() .
.
(1)求抛物线的解析式;
(2)如图1,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() 轴相交于点
轴相交于点![]() ,抛物线与
,抛物线与![]() 轴相交于点
轴相交于点![]() ,在直线
,在直线![]() 上有一点
上有一点![]() ,若
,若![]() ,求
,求![]() 的面积;
的面积;

(3)如图2,点![]() 是折线
是折线![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴,过点
轴,过点![]() 作
作![]() 轴,直线
轴,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,连接
,连接![]() ,将
,将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,若点
,若点![]() 落在
落在![]() 轴上,请直接写出
轴上,请直接写出![]() 点的坐标.
点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b,c在数轴上的位置如图所示,且表示数a的点、数b的点与原点的距离相等.
(1)用“>”“<”或“=”填空:b______0,a+b______0,a-c______0,b-c______0;
(2)|b-1|+|a-1|=________;
(3)化简:|a+b|+|a-c|-|b|+|b-c|.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
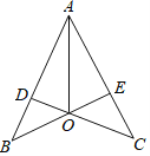
【题目】(1)一个不透明的盒子中装有 2 枚黑色的棋子和 1 枚白色的棋子,每枚棋子除了颜色外其余均相同.从盒中随机摸出一枚棋子,记下颜色后放回并搅匀,再从盒子中随机摸出一枚棋子,记下颜色,用画树状图(或列表)的方法,求两次摸出的棋子颜色不同的概率.
(2)如图,已知 ![]() ,
,![]() ,
,![]() ,
,![]() 交
交![]() 于点O,连接
于点O,连接![]() ,求证:AO平分
,求证:AO平分![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,有一个长方体,它的长、宽、高分别为5cm,3cm,4cm.在顶点A处有一只蚂蚁,它想吃到与顶点A相对的顶点B的食物.
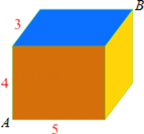
(1)请画出该蚂蚁沿长方体表面爬行的三条线路图(即平面展开图);
(2)已知蚂蚁沿长方体表面爬行的速度是0.8cm/s,问蚂蚁能否在11秒内获取到食物?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知P为锐角∠MAN内部一点,过点P作PB⊥AM于点B,PC⊥AN于点C,以PB为直径作⊙O,交直线CP于点D,连接AP,BD,AP交⊙O于点E.

(1)求证:∠BPD=∠BAC.
(2)连接EB,ED,当tan∠MAN=2,AB=2![]() 时,在点P的整个运动过程中.
时,在点P的整个运动过程中.
①若∠BDE=45°,求PD的长;
②若△BED为等腰三角形,求所有满足条件的BD的长;
(3)连接OC,EC,OC交AP于点F,当tan∠MAN=1,OC//BE时,记△OFP的面积为S1,△CFE的面积为S2,请写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 是线段
是线段![]() 上任一点,
上任一点,![]() ,
,![]() 两点分别从
两点分别从![]() 同时向
同时向![]() 点运动,且
点运动,且![]() 点的运动速度为
点的运动速度为![]() ,
,![]() 点的运动速度为
点的运动速度为![]() ,运动的时间为
,运动的时间为![]() .
.
(1)若![]() ,
,
①运动![]() 后,求
后,求![]() 的长;
的长;
②当![]() 在线段
在线段![]() 上运动时,试说明
上运动时,试说明![]() ;
;
(2)如果![]() 时,
时,![]() ,试探索
,试探索![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用火柴棒按下图的方式搭塔式三角形,第一个图用了3根火柴棒,第二个图用了9根火柴棒,第三个图用了18根火柴棒,......,照这样下去,第9个图用了_____根火柴棒.
 ……
……
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com