计算:$\root{3}{64}$+$^{-2}$=8．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

17．计算：$\root{3}{64}$+$（\frac{1}{2}）^{-2}$=8．

分析先算立方根和负整数指数幂，再相加即可求解．

解答解：$\root{3}{64}$+$（\frac{1}{2}）^{-2}$
=4+4
=8．
故答案为：8．

点评考查了立方根和负整数指数幂，关键是熟练掌握计算法则正确进行计算．

练习册系列答案

中考123基础章节总复习测试卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

20．折纸的思考．
【操作体验】
用一张矩形纸片折等边三角形．
第一步，对折矩形纸片ABCD（AB＞BC）（图①），使AB与DC重合，得到折痕EF，把纸片展平（图②）．
第二步，如图③，再一次折叠纸片，使点C落在EF上的P处，并使折痕经过点B，得到折痕BG，折出PB、PC，得到△PBC．
（1）说明△PBC是等边三角形．
【数学思考】
（2）如图④，小明画出了图③的矩形ABCD和等边三角形PBC．他发现，在矩形ABCD中把△PBC经过图形变化，可以得到图⑤中的更大的等边三角形，请描述图形变化的过程．
（3）已知矩形一边长为3cm，另一边长为a cm，对于每一个确定的a的值，在矩形中都能画出最大的等边三角形，请画出不同情形的示意图，并写出对应的a的取值范围．
【问题解决】
（4）用一张正方形铁片剪一个直角边长分别为4cm和1cm的直角三角形铁片，所需正方形铁片的边长的最小值为$\frac{16}{5}$cm．

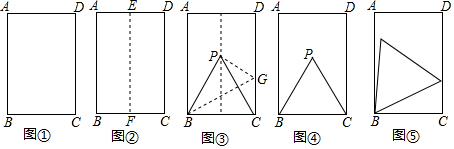
查看答案和解析>>

科目：初中数学 来源： 题型：填空题

8．在平面直角坐标系中，规定把一个点先绕原点逆时针旋转30°，再作出它关于原点的对称点称为一次变换．已知点A的坐标为（1，0），把点A经过连续2015次这样的变换得到的点A₂₀₁₅的坐标是（-$\frac{\sqrt{3}}{2}$，-$\frac{1}{2}$）．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

5．

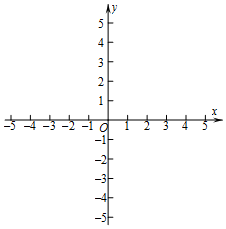已知：二次函数y=2x²+4x+m-1，与x轴的公共点为A，B．
（1）如果A与B重合，求m的值；
（2）横、纵坐标都是整数的点叫做整点；
①当m=1时，求线段AB上整点的个数；
②若设抛物线在点A，B之间的部分与线段AB所围成的区域内（包括边界）整点的个数为n，当1＜n＜8时，结合函数的图象，求m的取值范围．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

12．

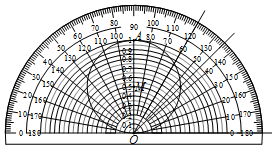利用量角器可以制作“锐角正弦值速查卡”．制作方法如下：如图，设OA=1，以O为圆心，分别以0.05，0.1，0.15，0.2，…，0.9，0.95长为半径作半圆，再以OA为直径作⊙M．利用“锐角正弦值速查卡”可以读出相应锐角正弦的近似值．例如：sin60°≈0.87，sin45°=0.71．下列角度中正弦值最接近0.94的是（　　）

A．

70°

B．

50°

C．

40°

D．

30°

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

2．

如图，⊙O是△ABC的外接圆，∠ACO=45°，则∠B的度数为45°．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

9．在综合实践话动课上，老师组织大家利用两块大小相同的含30°角的三角板进行拼接组合（不重叠）的探索活动，在讨论所组合而成的图形过程中，所得下列四个结论中错误的是（　　）

	A．	当两块三角板的斜边完全拼接在一起时，所拼成的图形一定是轴对称图形
	B．	当两块三角板的对应直角边完全拼接在一起时，所拼成的图形可能是等边三角形
	C．	当两块三角板可以通过平移后重合时，所拼成的图形不可能是轴对称图形
	D．	当两块三角板只有直角顶点拼接在一起时，所拼成的图形不可能是中心对称图形

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

6．下列图形中，既是轴对称图形，又是中心对称图形的是（　　）

A．