
【题目】如图1,![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,
,![]() ,
,![]() .
.
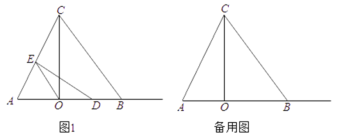
(1)求![]() ,
,![]() 的长
的长
(2)若点![]() 是射线
是射线![]() 上的一个动点,作
上的一个动点,作![]() 于点
于点![]() ,连结
,连结![]() .
.
①当点![]() 在线段
在线段![]() 上时,若
上时,若![]() 是以
是以![]() 为腰的等腰三角形,请求出所有符合条件的
为腰的等腰三角形,请求出所有符合条件的![]() 的长.
的长.
②设![]() 交直线
交直线![]() 于点
于点![]() ,连结
,连结![]() ,
,![]() ,若
,若![]() ,则
,则![]() 的长为______________.(直接写出结果)
的长为______________.(直接写出结果)
【答案】(1)BC=10,AC=![]() (2)①
(2)①![]() -4或4; ②
-4或4; ②![]() 或8
或8![]() .
.
【解析】
(1)根据BA=BC可得BC的长,分别根据勾股定理可得OC和AC的长;
(2)①分两种情况:AO=OE和AO=AE时,分别画图,根据三角形的中位线定理和证明三角形全等可解决问题;
②分两种情况:
i)当D在线段OB上时,如图3,过B作BG⊥EF于G,根据同高三角形面积的比等于对应底边的比,得![]() ,可得BF=
,可得BF=![]() ,根据平行线的性质证明∠BDG=∠BFG,得BD=BF=
,根据平行线的性质证明∠BDG=∠BFG,得BD=BF=![]() ,最后利用勾股定理可得结论;
,最后利用勾股定理可得结论;
ii)当D在线段OB的延长线上时,如图4,过B作BG⊥DE于G,同理计算可得结论.
(1)∵AO=4,BO=6,
∴AB=10,
∵BA=BC,
∴BC=10,
∵CO⊥AB,
∴∠AOC=∠BOC=90°,
∵![]()
∴![]()
(2)①分两种情况:
i)如图1,当AO=OE=4时,过O作ON⊥AC于N,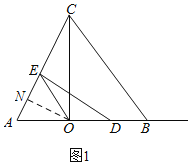
∴AN=EN,
∵DE⊥AC,
∴ON∥DE,
∴AO=OD=4;
ii)当AO=AE=4时,如图2,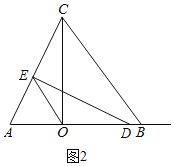
在△CAO和△DAE中,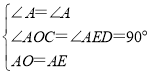 ,
,
∴△CAO≌△DAE(AAS),
∴AD=AC=4![]() ,
,
∴OD=4![]() -4;
-4;
②分两种情况:
i)当D在线段OB上时,如图3,过B作BG⊥EF于G,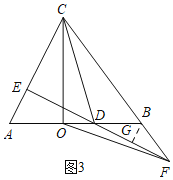
∵S△OBF:S△OCF=1:4,
∴![]()
∴![]()
∵CB=10
∴BF=![]()
∵EF⊥AC,
∴BG∥AC,
∴∠GBF=∠ACB,
∵AE∥BG,
∴∠A=∠DBG,
∵AB=BC,
∴∠A=∠ACB,
∴∠DBG=∠GBF,
∵∠DGB=∠FGB,
∴∠BDG=∠BFG,
∴BD=BF=![]() ,
,
∴OD=OB-BD=6-![]() =
=![]() ,
,
∴CD=![]() ;
;
ii)当D在线段OB的延长线上时,如图4,过B作BG⊥DE于G,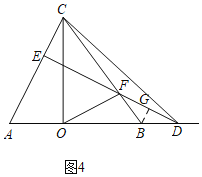
同理得![]() ,
,
∵BC=10,
∴BF=2,
同理得:∠BFG=∠BDF,
∴BD=BF=2,
Rt△COD中,CD=![]() ,
,
综上,CD的长为![]() 或8
或8![]() .
.
故答案为:![]() 或8
或8![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】小明用的练习本可在甲,乙两个商店买到,已知两个商店的标价都是每本1元.但甲商店的优惠条件是:购买10本以上,从第11本开始按标价七折卖;乙商店的优惠条件是:从第1本开始就按标价的八五折卖.若小明购买练习本数量为![]() 本,在甲商店购买后的总费用为
本,在甲商店购买后的总费用为![]() 元,在乙商店购买后的总费用为
元,在乙商店购买后的总费用为![]() 元.
元.
(1)写出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(2)小明要买20本练习本,到哪个商店购买较省钱?
(3)小明现有24元,最多可买多少本练习本?
查看答案和解析>>
科目:初中数学 来源: 题型:
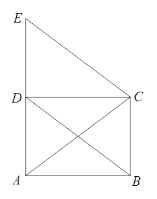
【题目】已知:如图,四边形ABCD是平行四边形,CE∥BD交AD的延长线于点E,CE=AC.
(1)求证:四边形ABCD是矩形;
(2)若AB=4,AD=3,求四边形BCED的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC内接于⊙O,AC是⊙O的直径,D是![]() 的中点.过点D作CB的垂线,分别交CB、CA延长线于点F、E.
的中点.过点D作CB的垂线,分别交CB、CA延长线于点F、E. 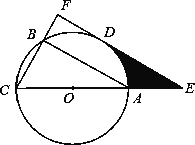
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若CF=6,∠ACB=60°,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校需要添置教师办公桌椅A、B两型共200套,已知2套A型桌椅和1套B型桌椅共需2000元,1套A型桌椅和3套B型桌椅共需3000元.
(1)求A,B两型桌椅的单价;
(2)若需要A型桌椅不少于120套,B型桌椅不少于70套,平均每套桌椅需要运费10元.设购买A型桌椅x套时,总费用为y元,求y与x的函数关系式,并直接写出x的取值范围;
(3)求出总费用最少的购置方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D在边BC上,点E在边AC上,且AD=AE.
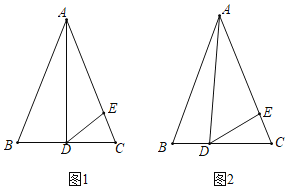
(1)如图1,当AD是边BC上的高,且∠BAD=30°时,求∠EDC的度数;
(2)如图2,当AD不是边BC上的高时,请判断∠BAD与∠EDC之间的关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
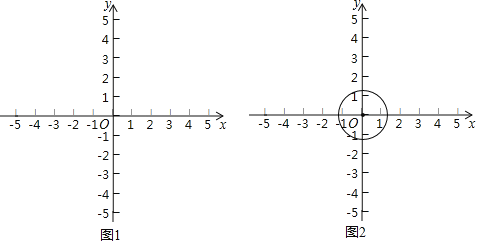
【题目】在平面直角坐标系xOy中,点M的坐标为(x1,y1),点N的坐标为(x2,y2),且x1≠x2,y1≠y2,以MN为边构造菱形,若该菱形的两条对角线分别平行于x轴,y轴,则称该菱形为边的“坐标菱形”.
(1)已知点A(1,0),B(0,![]() ),则以AB为边的“坐标菱形”的最小内角为______;
),则以AB为边的“坐标菱形”的最小内角为______;
(2)若点C(2,1),点D在直线y=5上,以CD为边的坐标菱形”为正方形,求育直线CD表达式;
(3)⊙O的半径为![]() ,点P的坐标为(3,m),若在⊙O上存在一点Q,使得以QP为边的“坐标菱形”为正方形,求m的取值范围.
,点P的坐标为(3,m),若在⊙O上存在一点Q,使得以QP为边的“坐标菱形”为正方形,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P是菱形ABCD的对角线BD上的一动点,连接CP并延长交AD于E,交BA的延长线于点F.
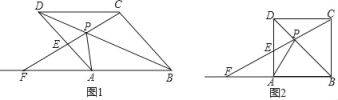
(1)求证:△APD≌△CPD;
(2)如图2,当菱形ABCD变为正方形,且PC=2,tan∠PFA=![]() 时,求正方形ABCD的边长.
时,求正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
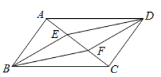
【题目】如图,在□ABCD中,E,F是对角线AC上的两点且AE=CF,在①BE=DF;②AB=DE;③BE∥DF;④四边形EBFD为菱形;⑤S△ADE=S△ABE;⑥AF=CE,这些结论中正确的是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com