
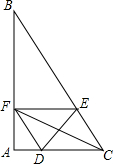
 如图,在△ABC中,∠A=90°,∠B=30°,AC=6cm,点D从点A开始以1cm/s的速度向点C运动,点E从点C开始以2cm/s的速度向点B运动,两点同时运动,同时停止,运动的时间为ts,过点E作EF∥AC交AB于点F.
如图,在△ABC中,∠A=90°,∠B=30°,AC=6cm,点D从点A开始以1cm/s的速度向点C运动,点E从点C开始以2cm/s的速度向点B运动,两点同时运动,同时停止,运动的时间为ts,过点E作EF∥AC交AB于点F.分析 (1)根据等边三角形的性质得到EC=DC,列方程得到t=2,
(2)根据直角三角形的性质得到CE=$\frac{1}{2}$DC,列方程得到2t=$\frac{1}{2}$(6-t),根据直角三角形的性质列方程得到结论;
(3)根据直角三角形的性质得到BC=12cm,于是得到DC=(6-t)cm,BE=(12-2t)cm,根据平行线的性质得到∠A=∠BFE=90°,由直角三角形的性质得到EF=$\frac{1}{2}$BE=$\frac{1}{2}$(12-2t)=(6-t)cm,即可得到结论;
(4)根据三角形的内角和得到∠ACB=60°,根据角平分线的定义得到∠ACF=∠BCF=30°,根据等腰三角形的判定得到BF=CF,等量代换即可得到结论.
解答 解:由题意得AD=tcm,CE=2tcm,
(1)若△DEC为等边三角形,则EC=DC,
∴2t=6-t,解得t=2,
∴当t为2时,△DEC为等边三角形;
(2)若△DEC为直角三角形,当∠CED=90°,
∴CE=$\frac{1}{2}$DC,
∴2t=$\frac{1}{2}$(6-t),
解得:t=1.2,
当∠CDE=90°时,∴$\frac{1}{2}$CE=DC,
∴$\frac{1}{2}×2t$=6-t,
∴t=3,
∴t为1.2或3时,△DEC为直角三角形;
(3)∵∠A=90°,∠B=30°,AC=6cm,
∴BC=12cm,
∴DC=(6-t)cm,BE=(12-2t)cm,
∵EF∥AC,
∴∠A=∠BFE=90°,
∵∠B=30°,
∴EF=$\frac{1}{2}$BE=$\frac{1}{2}$(12-2t)=(6-t)cm,
∴EF=CD;
(4)∵∠A=90°,∠B=30°,
∴∠ACB=60°,
∵CF平分∠ACB,
∴∠ACF=∠BCF=30°,
∴∠B=∠BCF,AF=$\frac{1}{2}$CF,
∴BF=CF,
∴BF=2AF.
点评 本题考查了等边三角形的性质,直角三角形的性质,角平分线的定义,等腰三角形的判定和性质,平行线的性质,正确的识别图形是解题的关键.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 3或5 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x2-3y-5=0 | B. | x2=2x | C. | $\frac{1}{x}$+4=x2 | D. | y2-$\sqrt{2y}$-3=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
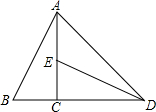 如图所示,将Rt△ABC绕其直角顶点C按顺时针方向旋转90°后得到Rt△DEC,连接AD,若∠BAC=25°,则∠ADE=( )
如图所示,将Rt△ABC绕其直角顶点C按顺时针方向旋转90°后得到Rt△DEC,连接AD,若∠BAC=25°,则∠ADE=( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 P是⊙O内一点,过点P作⊙O的任意一条弦AB,我们把PA•PB的值称为点P关于⊙O的“幂值”.
P是⊙O内一点,过点P作⊙O的任意一条弦AB,我们把PA•PB的值称为点P关于⊙O的“幂值”. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com