
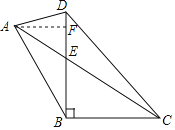
【题目】如图,在四边形ABCD中,∠DBC=90°,∠ABD=30°,∠ADB=75°,AC与BD交于点E,若CE=2AE=4![]() ,则DC的长为________.
,则DC的长为________.

【答案】![]()
【解析】
过A点作A⊥BD于F,根据平行线的判定可得AF∥BC,根据含30度直角三角形的性质可得BC=AB,根据三角形内角和可得∠ADB=∠BAD,根据等腰三角形的性质可得BD=AB,从而得到BC=BD,在Rt△CBE中,根据含30度直角三角形的性质可得BC,在Rt△CBD中,根据等腰直角三角形的性质可得CD.
过A点作A⊥BD于F,
∵∠DBC=90°,
∴AF∥BC,
∵CE=2AE,
∴AF=![]() BC,
BC,
∵∠ABD=30°,
∴AF=![]() AB,
AB,
∴BC=AB,
∵∠ABD=30°,∠ADB=75°,
∴∠BAD=75°,∠ACB=30°,
∴∠ADB=∠BAD,
∴BD=AB,
∴BC=BD,
∵CE=4![]() ,
,
在Rt△CBE中,BC=![]() CE=6,
CE=6,
在Rt△CBD中,CD=![]() BC=6
BC=6![]() .
.
故答案为:6![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在数轴上有三个点A,B,C,回答下列问题:
(1)若将点B向右移动6个单位后,三个点所表示的数中最小的数是多少?
(2)在数轴上找一点D,使点D到A,C两点的距离相等,写出点D表示的数;
(3)在点B左侧找一点E,使点E到点A的距离是到点B的距离的2倍,并写出点E表示的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
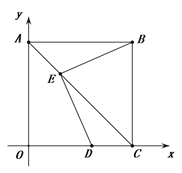
【题目】如图,在直角坐标系中,正方形ABCO的点B坐标(3,3),点A、C分别在y轴、x轴上,对角线AC上一动点E,连接BE,过E作DE⊥BE交OC于点D.若点D坐标为(2,0),则点E坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
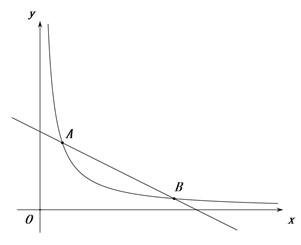
【题目】如图,一次函数y=-![]() x+b与反比例函数y=
x+b与反比例函数y=![]() (x>0)的图象交于点A(2,6)和B(m,1)
(x>0)的图象交于点A(2,6)和B(m,1)
(1)填空:一次函数的解析式为 ,反比例函数的解析式为 ;
(2)点E为y轴上一个动点,若S△AEB=5,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1、2、3分别表示甲、乙、丙三人由A地到B地的路线图,已知
甲的路线为:A→C→B;
乙的路线为:A→D→E→F→B,其中E为AB的中点;
丙的路线为:A→I→J→K→B,其中J在AB上,且AJ>JB.

若符号[→]表示[直线前进],则根据图1、图2、图3的数据,判断三人行进路线长度的大小关系为( )
A. 甲=乙=丙 B. 甲<乙<丙 C. 乙<丙<甲 D. 丙<乙<甲
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个图案均由边长相等的黑、白两色正方形按规律拼接而成,照此规律,第n个图案中白色正方形比黑色正方形多________个.(用含n的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地2016年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,2018年在2016年的基础上增加投入资金1600万元.
(1)从2016年到2018年,该地投入异地安置资金的年平均增长率为多少?
(2)在2018年异地安置的具体实施中,该地计划投入资金不低于500万元用于优先搬迁租房奖励,规定前800户(含第800户)每户每天奖励10元,800户以后每户每天奖励5元,按租房400天计算,求2018年该地至少有多少户享受到优先搬迁租房奖励.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线![]() 经过点A(-5.-6)且与直线
经过点A(-5.-6)且与直线![]() : y=-
: y=-![]() x+6平行,直线
x+6平行,直线![]() 与x轴、y轴分别交于点B,C
与x轴、y轴分别交于点B,C
(1)求直线![]() 的表达式及其与x轴的交点D的坐标:
的表达式及其与x轴的交点D的坐标:
(2)判断四边形ABCD是什么四边形?并证明你的结论:
(3)若点E是直线AB上一点,平面内存在一点F,使得四边形CBEF是正方形,求点E的坐标. 请直接写出答案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com