
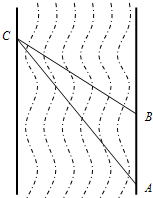
 小明同学需测量一条河流的宽度(河岸两边互相平行).如图,小明同学在河岸一侧选取两个观测点A、B,在河对岸选取观测点C,测得AB=31m,∠CAB=37°,∠CBA=120°.请你根据以上数据,帮助小明计算出这条河的宽度.
小明同学需测量一条河流的宽度(河岸两边互相平行).如图,小明同学在河岸一侧选取两个观测点A、B,在河对岸选取观测点C,测得AB=31m,∠CAB=37°,∠CBA=120°.请你根据以上数据,帮助小明计算出这条河的宽度.分析 要求CD的长,需要构造直角三角形,作CD⊥AB于点D,然后根据题目中的条件可以求得CD的长,本题得以解决.
解答 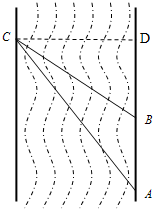 解:过点C作CD⊥AB,垂足为点D,如右图所示,
解:过点C作CD⊥AB,垂足为点D,如右图所示,
在Rt△CAD中,tan∠CAD=$\frac{CD}{AD}$,
∴AD=$\frac{CD}{tan∠CAD}$=$\frac{CD}{tan37°}$,
在Rt△CBD中,tan∠CBD=$\frac{CD}{BD}$,∠CBA=120°,
∴∠CBD=60°,
∴BD=$\frac{CD}{tan∠CBD}$=$\frac{CD}{tan60°}$,
∵AD-BD=AB,
∴$\frac{CD}{tan37°}$-$\frac{CD}{tan60°}$=31,
$\frac{CD}{0.75}$-$\frac{CD}{\sqrt{3}}$=31,
解得,CD≈41.0,
即这条河的宽度约为41.0米.
点评 本题考查解直角三角形的应用,解题的关键是明确题意,找出所求问题需要的条件,利用锐角三角函数进行解答.


科目:初中数学 来源: 题型:选择题
| A. | (4,-5) | B. | (4,5) | C. | (-5,-4) | D. | (5,-4) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
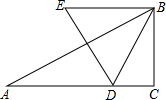 如图,己知△ABC中,∠C=90°,∠A=30°,AC=$\sqrt{3}$.动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为$\sqrt{3}$.
如图,己知△ABC中,∠C=90°,∠A=30°,AC=$\sqrt{3}$.动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
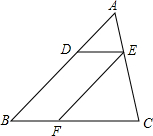 如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:AB=3:8,那么S△ADE:S△EFC=9:25.
如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:AB=3:8,那么S△ADE:S△EFC=9:25.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
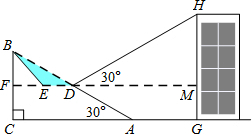 如图,已知斜坡AB长60m,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.732).
如图,已知斜坡AB长60m,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.732).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com