
【题目】如图,O是![]() 所在圆的圆心,C是
所在圆的圆心,C是![]() 上一动点,连接OC交弦AB于点D.已知AB=9.35cm,设A,D两点间的距离为
上一动点,连接OC交弦AB于点D.已知AB=9.35cm,设A,D两点间的距离为![]() cm,O,D两点间的距离为
cm,O,D两点间的距离为![]() cm,C,D两点间的距离为
cm,C,D两点间的距离为![]() cm.小腾根据学习函数的经验,分别对函数
cm.小腾根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.下面是小腾的探究过程,请补充完整:
的变化而变化的规律进行了探究.下面是小腾的探究过程,请补充完整:
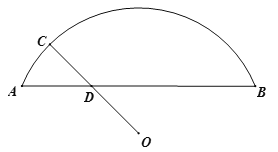
(1)按照下表中自变量![]() 的值进行取点、画图、测量,分别得到了
的值进行取点、画图、测量,分别得到了![]() ,
,![]() 与
与![]() 的几组对应值:
的几组对应值:
| 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 | 7.10 | 8.00 | 9.35 |
| 4.93 | 3.99 |
| 2.28 | 1.70 | 1.59 | 2.04 | 2.88 | 3.67 | 4.93 |
| 0.00 | 0.94 | 1.83 | 2.65 | 3.23 | 3.34 | 2.89 | 2.05 | 1.26 | 0.00 |
(2)①在同一平面直角坐标系![]() 中,描出表中各组数值所对应的点(
中,描出表中各组数值所对应的点(![]() ,
,![]() ), (
), (![]() ,
,![]() ),并画出(1)中所确定的函数
),并画出(1)中所确定的函数![]() ,
,![]() 的图象;
的图象;
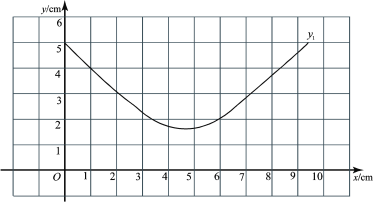
②观察函数![]() 的图象,可得
的图象,可得![]() cm(结果保留一位小数);
cm(结果保留一位小数);
(
科目:初中数学 来源: 题型:
【题目】某中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.
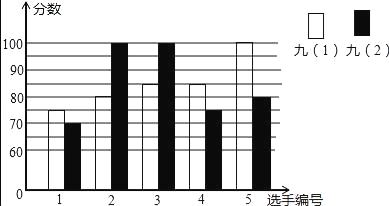
(1)根据图示填写下表:
班级 | 中位数(分) | 众数(分) |
九(1) | 85 | |
九(2) | 100 |
(2)通过计算得知九(2)班的平均成绩为85分,请计算九(1)班的平均成绩.
(3)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好.
(4)已知九(1)班复赛成绩的方差是70,请计算九(2)班的复赛成绩的方差,并说明哪个班的成绩比较稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
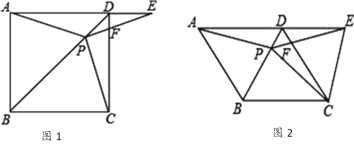
【题目】如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:△APD≌△CPD;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“过圆外一点作这个圆的两条切线”的尺规作图过程.
已知:⊙O及⊙O外一点P.
求作:直线PA和直线PB,使PA切⊙O于点A,PB切⊙O于点B.
作法:如图,
①连接OP,分别以点O和点P为圆心,大于![]() OP的同样长为半径作弧,两弧分别交于点M,N;
OP的同样长为半径作弧,两弧分别交于点M,N;
②连接MN,交OP于点Q,再以点Q为圆心,OQ的长为半径作弧,交⊙O于点A和点B;
③作直线PA和直线PB.
所以直线PA和PB就是所求作的直线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
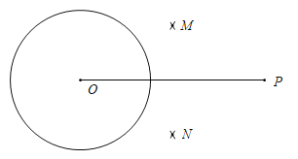
(2)完成下面的证明.
证明:∵OP是⊙Q的直径,
∴ ∠OAP=∠OBP=________°( )(填推理的依据).
∴PA⊥OA,PB⊥OB.
∵OA,OB为⊙O的半径,
∴PA,PB是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中,已知点A(-2,0)和点B(3,0),线段AB和线段AB外的一点P,给出如下定义:若45°≤∠APB≤90°时,则称点P为线段AB的可视点,且当PA=PB时,称点P为线段AB的正可视点.
中,已知点A(-2,0)和点B(3,0),线段AB和线段AB外的一点P,给出如下定义:若45°≤∠APB≤90°时,则称点P为线段AB的可视点,且当PA=PB时,称点P为线段AB的正可视点.


图1 备用图
(1) ①如图1,在点P1(3,6),P2(-2,-5),P3(2,2)中,线段AB的可视点是 ;
②若点P在y轴正半轴上,写出一个满足条件的点P的坐标:__________.
(2)在直线y=x+b上存在线段AB的可视点,求b的取值范围;
(3)在直线y=-x+m上存在线段AB的正可视点,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象如图所示,则下列结论:①
的图象如图所示,则下列结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() :④方程
:④方程![]()
![]() 有两个大于-1的实数根.其中正确的是( )
有两个大于-1的实数根.其中正确的是( )
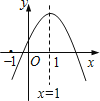
A.①②③B.①②④C.②③④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=![]() x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.
x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.
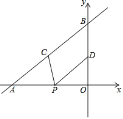
A. (-3,0) B. (-6,0) C. (-![]() ,0) D. (-
,0) D. (-![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,点E是AB上一点,且AE=2EB .
(1)求![]() 的值.
的值.
(2)求![]() 的值.
的值.
(3)如果△AEF的面积![]() =8cm2,分别求出△CDF的面积
=8cm2,分别求出△CDF的面积![]() 和△ADF的面积
和△ADF的面积![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利川市南门大桥是上世纪90年代修建的一座石拱桥,其主桥孔的横截面是一条抛物线的一部分,2019年在维修时,施工队测得主桥孔最高点![]() 到水平线
到水平线![]() 的高度为
的高度为![]() .宽度
.宽度![]() 为
为![]() .如图所示,现以
.如图所示,现以![]() 点为原点,
点为原点,![]() 所在直线为
所在直线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.

(1)直接写出点![]() 及抛物线顶点
及抛物线顶点![]() 的坐标;
的坐标;
(2)求出这条抛物线的函数解析式;
(3)施工队计划在主桥孔内搭建矩形“脚手架”![]() ,使
,使![]() 点在抛物线上,
点在抛物线上,![]() 点在水平线
点在水平线![]() 上,为了筹备材料,需求出“脚手架”三根钢管
上,为了筹备材料,需求出“脚手架”三根钢管![]() 的长度之和的最大值是多少?请你帮施工队计算.
的长度之和的最大值是多少?请你帮施工队计算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com