练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，矩形ABCD和正方形EFGH的中心重合，，，分别延长FE，GF，HG和EH交AB，BC，CD，AD于点I，J，K，若，则AI的长为______，四边形AIEL的面积为______．

    【答案】5；

    【解析】

    根据题意延长LE交BC于M，延长JG交AD于T，延长KH交AB于R，延长IF交CD于W，作于N，于Z，于S，于根据对称性，解直角三角形即可解决问题；

    延长LE交BC于M，延长JG交AD于T，延长KH交AB于R，延长IF交CD于W，作于N，于Z，于S，于Q．

    矩形ABCD和正方形EFGH的中心重合，
    根据对称性可知：，，，，
    四边形ABMN，四边形BCWS，四边形EHQI，四边形GHLZ都是矩形，
    ，，
    由题意：在中，，
    ，，
    在中，，，
    ，，
    ，
    ，，
    同法可得，，，
    四边形AIEL的面积为，
    故答案为5，．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，点E在等边△ABC的边BC上，BE＝6，射线CD⊥BC于点C，点P是射线CD上一动点，点F是线段AB上一动点，当EP+PF的值最小时，BF＝7，则AC为______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

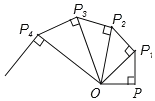
    【题目】如图，OP=1，过P作PP1⊥OP，得OP1=；再过P1作P1P2⊥OP1且P1P2=1，得OP2=；又过P2作P2P3⊥OP2且P2P3=1，得OP3=2；…依次法继续作下去，S1，S2，S3…分别表示各个三角形的面积，那么S12+S22+S32+…+S92的值是（　　）

    A.B.C.D.55

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠A=30°，∠B=60°，CF平分∠ACB．

    （1）求∠ACE的度数．

    （2）若CD⊥AB于点D，∠CDF=75°，求证：△CFD是直角三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，CD是一高为4米的平台，AB是与CD底部相平的一棵树，在平台顶C点测得树顶A点的仰角α=30°，从平台底部向树的方向水平前进3米到达点E，在点E处测得树顶A点的仰角β=60°，求树高AB（结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知点、在直线上，点在线段上，与交于点，，．

    （1）请说明：；

    （2）若，，求的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

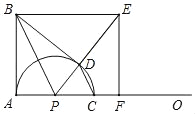
    【题目】如图，∠BAO=90°，AB=8，动点P在射线AO上，以PA为半径的半圆P交射线AO于另一点C，CD∥BP交半圆P于另一点D，BE∥AO交射线PD于点E，EF⊥AO于点F，连接BD，设AP=m．

    （1）求证：∠BDP=90°．

    （2）若m=4，求BE的长．

    （3）在点P的整个运动过程中．

    ①当AF=3CF时，求出所有符合条件的m的值．

    ②当tan∠DBE=时，直接写出△CDP与△BDP面积比．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知中，AB=AC=10 cm，BC=8cm，点D是AB的中点，点E在AC上，AE=6 cm，点P在BC上以1 cm/s速度由B点向C点运动，点Q在AC上由A点向E点运动，两点同时出发，当其中一点到达终点时，两点同时停止运动.

    （1）在运动过程中，若点Q速度为2 cm/s，则能否形成以为顶角的等腰三角形？若可以，请求出运动时间t， 若不可以，请说明理由；

    （2）当点Q速度为多少时，能够使 与全等？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，Rt△ABC纸片中，∠C=90°，AC=3，BC=4，点D在边BC上，以AD为折痕将△ABD折叠得到△AB’D，AB'与边BC交于点E．若△DEB’为直角三角形，则BD的长是________．

    查看答案和解析>>

    同步练习册答案