

分析 (1)首先作线段OA的中垂线交抛物线于点D,交OA于点G,连接OD、AD,然后求出点A的坐标是(8,0),再根据△OAD为等腰直角三角形,且点D在x轴上方的抛物线上,判断出线段OA不能是△OAD的直角边,只能是△OAD的斜边,据此求出点D的坐标即可.
(2)首先设在直线AD的上方的抛物线上点C的坐标为(m,-$\frac{1}{4}$m2+2m),根据三角形的面积的求法,用含有m的算式表示出S△ACD的大小,然后根据二次函数最值的求法,求出当m取什么值时,△ACD的面积最大,进而求出点C的坐标是多少;最后应用待定系数法,求出直线OC的解析式即可.
(3)根据题意,分类讨论:①当RQ=RN=$\frac{3}{2}$时;②当BG所在的直线为矩形RQMN的对称轴时;③当RQ与BG重合时;④当点R落在BF上时;然后根据矩形RQMN与△OBF重叠部分为轴对称图形以及RN=$\frac{3}{2}$,求出矩形RQMN与△OBF重叠部分为轴对称图形时点P的横坐标的取值范围即可.
解答 解:(1)如图1,作线段OA的中垂线交抛物线于点D,交OA于点G,连接OD、AD,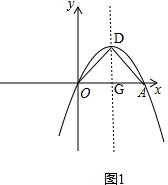 ,
,
∵抛物线y=-$\frac{1}{4}$x2+2x与x轴正半轴交于点A,
∴点A的坐标是(8,0),
∵△OAD为等腰直角三角形,且点D在x轴上方的抛物线上,
∴线段OA不能是△OAD的直角边,只能是△OAD的斜边,
∵△OAD为等腰直角三角形,DG⊥OA,
∴OG=GA=DG=4,∠ODA=90°,
∴点D的坐标为(4,4).
(2)如图2,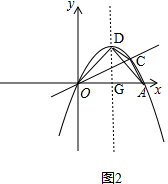 ,
,
设在直线AD的上方的抛物线上点C的坐标为(m,-$\frac{1}{4}$m2+2m),
则S△ACD=$\frac{1}{2}$(DG+|yC|)×|xC-xD|+$\frac{1}{2}$|yC|×|xA-xC|-$\frac{1}{2}$GA•DG
=$\frac{1}{2}$(4+|-$\frac{1}{4}$m2+2m|)×|m-4|+$\frac{1}{2}$×|-$\frac{1}{4}$m2+2m|×|8-m|-$\frac{1}{2}$×4×4
=-$\frac{1}{2}$m2+6m-16
=-$\frac{1}{2}$(m-6)2+2
∵4≤m≤8,
∴当m=6时,△ACD的面积最大,
∵当m=6时,
-$\frac{1}{4}$m2+2m=-$\frac{1}{4}$×62+2×6=3,
∴点C的坐标为C(6,3),
设直线OC的解析式为y=kx,
则6x=3,
解得k=$\frac{1}{2}$,
∴当△ACD的面积最大时,直线OC的解析式为y=$\frac{1}{2}$x.
(3)①如图3,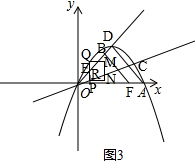 ,
,
当RQ=RN=$\frac{3}{2}$时,
设点P的坐标是(m,0),
则点Q的坐标是(m,-$\frac{1}{4}$m2+2m),点R的坐标是(m,$\frac{1}{2}m$),
∵-$\frac{1}{4}$m2+2m-$\frac{1}{2}m$=$\frac{3}{2}$,
∴m2-6m+6=0,
解得m=3+$\sqrt{3}$,m=3-$\sqrt{3}$,
∵点D的坐标是(4,4),m=3+$\sqrt{3}$>4,不符合题意,
∴m=3-$\sqrt{3}$.
②如图4,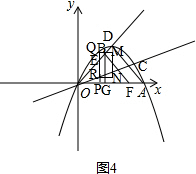 ,
,
当BG所在的直线为矩形RQMN的对称轴时,
设点P的坐标是(m,0),
∵点D的坐标为D(4,4),
∴OD=4$\sqrt{2}$,
∵$\frac{OB}{OD}$=$\frac{3}{4}$,
∴OB=$\frac{3}{4}×4\sqrt{2}$=3$\sqrt{2}$,
∴点B的坐标是(3,3),
∵RN=$\frac{3}{2}$,
∴$2(3-m)=\frac{3}{2}$,
解得m=$\frac{9}{4}$.
③如图5,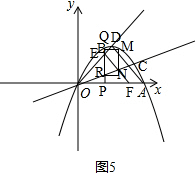 ,
,
当RQ与BG重合时,重叠部分为等腰直角三角形,
设点P的坐标是(m,0),
∵点D的坐标为D(4,4),
∴OD=4$\sqrt{2}$,
∵$\frac{OB}{OD}$=$\frac{3}{4}$,
∴OB=$\frac{3}{4}×4\sqrt{2}$=3$\sqrt{2}$,
∴点B的坐标是(3,3),
∴点P的坐标是(3,0),
即m=3.
④如图6, ,
,
当点R落在BF上时,
设点P的坐标是(m,0),
∵点D的坐标是(4,4),
∴OD所在的直线的解析式是:y=x,
∵FB⊥OD,
∴FB所在的直线的斜率是-1,
设FB所在的直线的解析式是y=-x+p,
则3=-3+p,
解得p=6,
∴FB所在的直线的解析式是y=-x+6,
联立$\left\{\begin{array}{l}{y=\frac{1}{2}x}\\{y=-x+6}\end{array}\right.$
可得$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$
∴点P的坐标是(4,0),
即m=4,
∴3≤m<4.
综上,可得
矩形RQMN与△OBF重叠部分为轴对称图形时点P的横坐标的取值范围是:
m=3-$\sqrt{3}$,m=$\frac{9}{4}$,或3≤m<4.
点评 (1)此题主要考查了二次函数综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合思想的应用,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力.
(2)此题还考查了待定系数法求直线解析式的方法,要熟练掌握.
(3)此题还考查了三角形的面积的求法,以及轴对称图形的性质和应用,要熟练掌握.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{{m}^{2}n}{4}$不是整式 | B. | -$\frac{3abc}{2}$的系数是-3,次数是3 | ||
| C. | 3是单项式 | D. | 多项式2x2y-xy是五次二项式 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}x=3\\ y=2\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=3\\ y=4\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=5\\ y=10\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=6\\ y=8\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
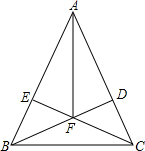 如图,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.试说明AF平分∠BAC的理由.
如图,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.试说明AF平分∠BAC的理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com