
【题目】解不等式组 ,请结合题意填空,完成本题的解答.
,请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得_________;
(Ⅱ)解不等式②,得_________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为_________.
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
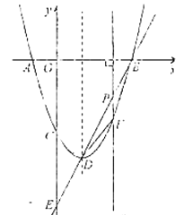
(Ⅰ)求顶点![]() 的坐标;
的坐标;
(Ⅱ)如图,设点![]() 为线段
为线段![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线与抛物线交于点
轴的垂线与抛物线交于点![]() .求
.求![]() 的面积最大值;
的面积最大值;
(Ⅲ)点![]() 在线段
在线段![]() 上,当
上,当![]() 时,求点
时,求点![]() 的坐标(直接写出结果,不必写解答过程).
的坐标(直接写出结果,不必写解答过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3经过点A(1,0)和点B(﹣3,0),与y轴交于点C,点P为第二象限内抛物线上的动点.
(1)抛物线的解析式为 ,抛物线的顶点坐标为 ;
(2)如图1,连接OP交BC于点D,当S△CPD:S△BPD=1:2时,请求出点D的坐标;
(3)如图2,点E的坐标为(0,﹣1),点G为x轴负半轴上的一点,∠OGE=15°,连接PE,若∠PEG=2∠OGE,请求出点P的坐标;
(4)如图3,是否存在点P,使四边形BOCP的面积为8?若存在,请求出点P的坐标;若不存在,请说明理由.
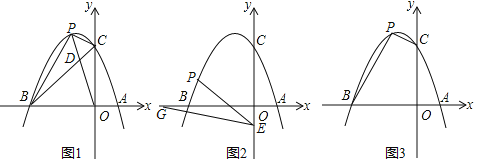
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是大小相等的边长为1的正方形构成的网格,![]() ,
,![]() ,
,![]() ,
,![]() 均为格点.
均为格点.![]() 与
与![]() 交于点
交于点![]() .
.
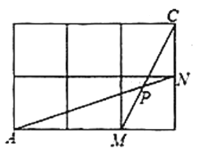
[1].![]() 的值为_________.
的值为_________.
[2].现只有无刻度的直尺,请在给定的网格中作出一个格点三角形.要求:①三角形中含有与![]() 大小相等的角;②可借助该三角形求得
大小相等的角;②可借助该三角形求得![]() 的三角函数值.请并在横线上简单说明你的作图方法.____________.
的三角函数值.请并在横线上简单说明你的作图方法.____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器商场销售A,B两种型号计算器,两种计算器的进货价格分别为每台30元,40元. 商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利120元.
(1)求商场销售A,B两种型号计算器的销售价格分别是多少元?(利润=销售价格﹣进货价格)
(2)商场准备用不多于2500元的资金购进A,B两种型号计算器共70台,问最少需要购进A型号的计算器多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
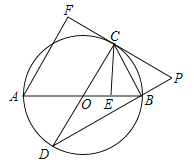
【题目】(2017广东省)如图,AB是⊙O的直径,AB=![]() ,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.
,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.
(1)求证:CB是∠ECP的平分线;
(2)求证:CF=CE;
(3)当![]() 时,求劣弧
时,求劣弧![]() 的长度(结果保留π)
的长度(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个两位数十位、个位上的数字分别为![]() ,我们可将这个两位数记为
,我们可将这个两位数记为![]() ,易知
,易知![]() ;同理,一个三位数、四位数等均可以用此记法,如
;同理,一个三位数、四位数等均可以用此记法,如![]() .
.
(基础训练)
(1)解方程填空:
①若![]() ,则
,则![]() ______;
______;
②若![]() ,则
,则![]() ______;
______;
③若![]() ,则
,则![]() ______;
______;
(能力提升)
(2)交换任意一个两位数![]() 的个位数字与十位数字,可得到一个新数
的个位数字与十位数字,可得到一个新数![]() ,则
,则![]() 一定能被______整除,
一定能被______整除,![]() 一定能被______整除,
一定能被______整除,![]() +++6一定能被______整除;(请从大于5的整数中选择合适的数填空)
+++6一定能被______整除;(请从大于5的整数中选择合适的数填空)
(探索发现)
(3)北京时间2019年4月10日21时,人类拍摄的首张黑洞照片问世,黑洞是一种引力极大的天体,连光都逃脱不了它的束缚.数学中也存在有趣的黑洞现象:任选一个三位数,要求个、十、百位的数字各不相同,把这个三位数的三个数字按大小重新排列,得出一个最大的数和一个最小的数,用得出的最大的数减去最小的数得到一个新数(例如若选的数为325,则用532-235=297),再将这个新数按上述方式重新排列,再相减,像这样运算若干次后一定会得到同一个重复出现的数,这个数称为“卡普雷卡尔黑洞数”.
①该“卡普雷卡尔黑洞数”为______;
②设任选的三位数为![]() (不妨设
(不妨设![]() ),试说明其均可产生该黑洞数.
),试说明其均可产生该黑洞数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com