
【题目】(本题满分6分)某公司调查某中学学生对其环保产品的了解情况,随机抽取该校部分学生进行问卷,结果分“非常了解”、“比较了解”、“一般了解”、“不了解”四种类型,分别记为A、B、C、D.根据调查结果绘制了如下尚不完整的统计图. 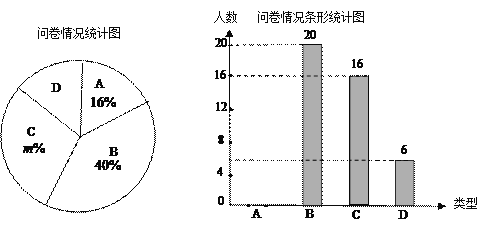
(1)本次问卷共随机调查了 名学生,扇形统计图中m= .
(2)请根据数据信息补全条形统计图;
(3)若该校有1000名学生,估计选择“非常了解”、“比较了解”共约有多少人?
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】某市为了节约用水,对自来水的收费标准作如下规定:每月每户用水不超过10吨的部分,按2元/吨收费;超过10吨的部分按2.5元/吨收费.
(1)若黄老师家5月份用水16吨,问应交水费多少元?
(2)若黄老师家6月份交水费30元,问黄老师家5月份用水多少吨?
(3)若黄老师家7月用水a吨,问应交水费多少元?(用a的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOC与∠BOD都是直角,则下列说法正确的是( )
①若∠COD=30°,则∠AOB=150°
②∠BOC=∠AOB﹣∠BOD
③∠AOD=∠BOC
④∠AOB与∠DOC的和不变
⑤∠AOB与∠DOC的和随∠DOC的变小而增大.
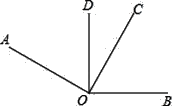
A. ①③④ B. ①②③④ C. ①③⑤ D. ①②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组 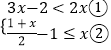 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得
(Ⅱ)解不等式②,得
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
(Ⅳ)原不等式组的解集为 ![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,O(0,0),A(7,0),B(5,2),C(0,2)一条动直线l分别与BC、OA交于 点E、F,且将四边形OABC分为面积相等的两部分,则点C到动直线l的距离的最大值为____,
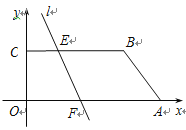
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八达岭森林体验中心,由八达岭森林体验馆和450公顷的户外体验区构成。森林体验馆包括"八达岭森林变迁"、"八达岭森林大家族"、"森林让生活更美好"等展厅,户外游憩体验系统根据森林生态旅游最新理念,采取少设施、设施集中的点线布局模式,突破传统的"看风景"旅游模式,强调全面体验森林之美。
在室内展厅内,有这样一个可以动手操作体验的仪器,如图小明在社会大课堂活动中,记录了这样一组数字:

交通 工具 | 行驶100公里的碳足迹(Kg) | 100公里碳中 和树木棵树 |
飞机 | 13.9 | 0.06 |
小轿车 | 22.5 | 0.10 |
公共汽车 | 1.3 | 0.005 |
根据以上材料回答问题:
A,B两地相距300公里,小轿车以90公里/小时的速度从A地开往B地;公共汽车以60公里/小时的速度从B开往A地,两车同时出发相对而行,两车在C地相遇,相遇后继续前行到达各自的目的地。
(1)多少小时后两车相遇?
(2)小轿车和公共汽车分别到达目的地,计算小轿车的碳足迹为多少?公共汽车的碳中和树木棵数为多少?
(3)根据观察或计算说明,为了减少环境污染,我们应该选择哪种交通工具出行更有利于环保呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,假设航空母舰始终以200千米/时的速度由西向东航行,飞机以800千米/时的速度从舰上起飞,向西航行执行任务,如果飞机在空中最多能连续飞行3个小时,那么它在起飞_____小时后就必须返航,才能安全停在舰上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形纸片ABCD中,AD=8,AB=6,E是边BC上的点,将纸片沿AE折叠,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
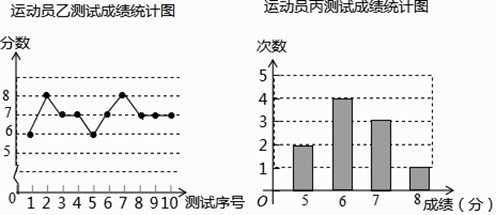
(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么?(参考数据:三人成绩的方差分别为S甲2=0.8、S乙2=0.4、S丙2=0.8)
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(用树状图或列表法解答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com