练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．我国古代数学家利用“牟合方盖”找到了球体体积的计算方法．“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体，如图所示的几何体是可以形成“牟合方盖”的一种模型，它的主视图是（　　）
    A．B．C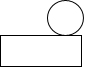．D．

    分析 根据主视图的定义，得出圆柱以及立方体的摆放即可得出主视图为3个正方形组合体，进而得出答案即可．

    解答 解：利用圆柱直径等于立方体边长，得出此时摆放，圆柱主视图是正方形，
    得出圆柱以及立方体的摆放的主视图为两列，左边一个正方形，右边两个正方形，
    故选：B．

    点评 此题主要考查了几何体的三视图；掌握主视图是从几何体正面看得到的平面图形是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．解不等式组$\left\{{\begin{array}{l}{3x-2＜2x+2}\\{6-x≥1-3（x-1）}\end{array}}\right.$，并在数轴上表示不等式组的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

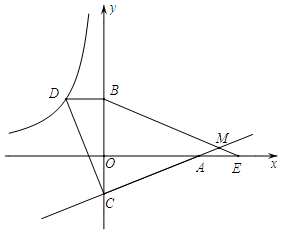    1．如图，已知点D在反比例函数y=$\frac{m}{x}$的图象上，过点D作x轴的平行线交y轴于点B（0，3），过点A（5，0）的直线y=kx+b与y轴于点C，且BD=OC，tan∠OAC=$\frac{2}{5}$．
    （1）求反比例函数y=$\frac{m}{x}$和直线y=kx+b的解析式；
    （2）连接CD，试判断线段AC与线段CD的关系，并说明理由；
    （3）点E为x轴上点A右侧的一点，且AE=OC，连接BE交直线CA于点M，求∠BMC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

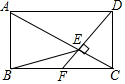    18．如图，在矩形ABCD中，F是BC边的中点，DF⊥AC，垂足为点E，连接BE，分析下列四个结论：①△CEF∽△CBA；②BE=AB；③AE=2CE；④tan∠ACB=$\sqrt{2}$，其中正确的个数有（　　）
    A．4个B．3个C．2个D．1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

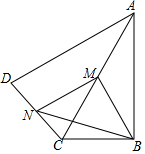    5．如图，在四边形ABCD中，∠ABC=90°，AC=AD，M，N分别为AC，CD的中点，连接BM，MN，BN．
    （1）求证：BM=MN；
    （2）若∠BAD=60°，AC平分∠BAD，AC=2，写出求BN长的思路．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．以下问题，不适合用全面调查的是（　　）
    A．旅客上飞机前的安检B．学校招聘教师，对应聘人员的面试
    C．了解全校学生的课外读书时间D．了解全国中学生的用眼卫生情况

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．某校1200名学生参加了全市得到“读数”活动，该校随机选取部分学生，对他们在三、四两个月的读数时间进行调查，并根据调查数据制作统计表和如图所示的频数分布直方图，均不完整，解答下列问题．
           四月日人均读书时间的统计表
     日人均读书时间x/h 人数/人 百分比
     0≤x≤0.5 6 
     0.5＜x≤1 30 
     1＜x≤1.5  50%
     1.5＜x≤2 10 10%
     2＜x≤2.5 bc 
    （1）本次调查的学生人数为100人；
    （2）图表中的a，b，c的值分别为6，4，4%；
    （3）在被调查的学生中，四月份日人均读书时间在1＜x≤1.5范围内的人数比三月份在此范围内的人数多44人；
    （4）试估计该校学生四月份人均读书时间在1小时以上的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．|-16|的算术平方根是4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

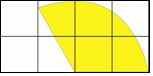    2．在如图所示的网格中，每个小正方形的边长都为1，若以小正形的顶点为圆心，2为半径作一个扇形围成一个圆锥，则所围成的圆锥的底面圆的半径为$\frac{2}{3}$．

    查看答案和解析>>

    同步练习册答案