
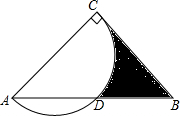
 如图,在等腰Rt△ABC中,∠ACB=90°,AC=4,以边AC为直径的半圆交AB于点D,则图中阴影部分的面积是6-π(结果保留π)
如图,在等腰Rt△ABC中,∠ACB=90°,AC=4,以边AC为直径的半圆交AB于点D,则图中阴影部分的面积是6-π(结果保留π)  海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:解答题
 如图,△A1B1C1由△ABC绕某点旋转而成,请你用尺规作图,找出旋转中心O,并用量角器度量出旋转的大小(完成填空).旋转角(∠COC1)是90度.
如图,△A1B1C1由△ABC绕某点旋转而成,请你用尺规作图,找出旋转中心O,并用量角器度量出旋转的大小(完成填空).旋转角(∠COC1)是90度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,小月家有四边形的田地ACBD,测量得∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=80cm,求这块菜地的面积是多少?
如图所示,小月家有四边形的田地ACBD,测量得∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=80cm,求这块菜地的面积是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com