
| A. | 2<x<18 | B. | 1<x<9 | C. | 0<x<10 | D. | 0<x<8 |
分析 由平行四边形的性质得出OA=OB=$\frac{1}{2}$AC=4,OB=OD=$\frac{1}{2}$BD=5,在△AOB中,由三角形的三边关系得出1<AB<9,同理1<BC<9,即可得出结果.
解答 解:如图所示:
∵四边形ABCD是平行四边形,
∴OA=OB=$\frac{1}{2}$AC=4,OB=OD=$\frac{1}{2}$BD=5,AB=CD,BC=AD,
在△AOB中,由三角形的三边关系得:5-4<AB<5+4,
即1<AB<9,
同理1<BC<9,
∴平行四边形ABCD每一边长x的取值范围是1<x<9,
故选:B.
点评 本题考查了平行四边形的性质、三角形的三边关系定理;熟练掌握平行四边形的性质,并能进行推理计算是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥-2 且x≠3 | B. | x≥-2 | C. | x≤-2且x≠0 | D. | x>-2且x≠3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 数据-2,1,3,4,4,5的中位数是4 | |
| B. | 想了解某种饮料中含色素的情况,宜采用抽样调查 | |
| C. | 数据1,1,2,2,3的众数是3 | |
| D. | 一组数据的波动越大,方差越小 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
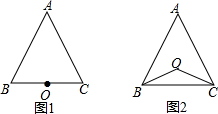 已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com