
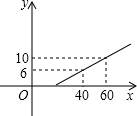
 某长途汽车客运公司规定旅客可免费携带一定质量的行李,当行李的质量超过规定时,需要购买行李票.已知行李费y(元)是行李质量x(kg)之间的函数表达式为y=kx+b.这个函数的图象如图所示:
某长途汽车客运公司规定旅客可免费携带一定质量的行李,当行李的质量超过规定时,需要购买行李票.已知行李费y(元)是行李质量x(kg)之间的函数表达式为y=kx+b.这个函数的图象如图所示: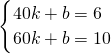 ,
, ;
; x-2=0,
x-2=0, x-2=4,解得x=30,
x-2=4,解得x=30, x-2=15,解得x=85,
x-2=15,解得x=85,

科目:初中数学 来源: 题型:
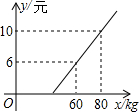 某长途汽车客运公司规定旅客可随身携带一定质量的行李,如果超过规这质量,则需购买行李费,如图是行李费y元是行李质量xkg的一次函数,那么旅客可携带的免费行李的最大质量为( )
某长途汽车客运公司规定旅客可随身携带一定质量的行李,如果超过规这质量,则需购买行李费,如图是行李费y元是行李质量xkg的一次函数,那么旅客可携带的免费行李的最大质量为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com