
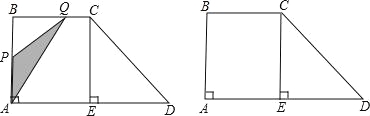
【题目】如图,梯形ABCD中,AD∥BC,∠BAD=90°,CE⊥AD于点E,AD=8cm<BC=4cm,AB=5cm,从初始时刻开始,动点P,Q分别从点A,B同时出发,运动速度均为1cm/s,动点P沿A﹣﹣B﹣﹣C﹣﹣E的方向运动,到点E停止;动点Q沿B﹣﹣C﹣﹣E﹣﹣D的方向运动,到点D停止,设运动时间为xs,△PAQ的面积为ycm2,(这里规定:线段是面积为0的三角形)解答下列问题:
(1)当x=2s时,y= cm2;当x=![]() s时,y= cm2;
s时,y= cm2;
(2)当5≤x≤14时,求y与x之间的函数关系式;
(3)直接写出在整个运动过程中,使PQ与四边形ABCE的对角线平行的所有x的值.
【答案】(1)2;9;(2)见试题解析;(3)由题意得x的值为:x=![]() 、
、![]() 或
或![]() .
.
【解析】
试题分析:(1)当x=2s时,AP=2,BQ=2,利用三角形的面积公式直接可以求出y的值,当x=![]() s时,三角形PAQ的高就是4,底为4.5,由三角形的面积公式可以求出其解.
s时,三角形PAQ的高就是4,底为4.5,由三角形的面积公式可以求出其解.
(2)当5≤x≤14 时,求y与x之间的函数关系式.要分为三种不同的情况进行表示:当5≤x≤9时,当9<x≤13时,当13<x≤14时.
(3)利用相似三角形的性质,相似三角形的对应线段成比例就可以求出对应的x的值.
试题解析:(1)当x=2s时,AP=2,BQ=2,∴y=2
当x=![]() s时,AP=4.5,Q点在EC上∴y=9
s时,AP=4.5,Q点在EC上∴y=9
故答案为:2;9
(2)当5≤x≤9时
y=S梯形ABCQ﹣S△ABP﹣S△PCQ=![]() (5+x﹣4)×4﹣
(5+x﹣4)×4﹣![]() ×5(x﹣5﹣
×5(x﹣5﹣![]() (9﹣x)(x﹣4)
(9﹣x)(x﹣4)
y=![]() x2﹣7x+
x2﹣7x+![]()
当9<x≤13
y=![]() (x﹣9+4)(14﹣x)
(x﹣9+4)(14﹣x)
y=﹣![]() x2+
x2+![]() x﹣35
x﹣35
当13<x≤14时
y=![]() ×8(14﹣x)
×8(14﹣x)
y=﹣4x+56;
(3)设运动时间为x秒,
当PQ∥AC时,BP=5﹣x,BQ=x,
此时△BPQ∽△BAC,∴![]() ,∴
,∴![]() ,解得x=
,解得x=![]() ;
;
当PQ∥BE时,PC=9﹣x,QC=x﹣4,此时△PCQ∽△BCE,∴![]() ,∴
,∴![]() ,
,
解得x=![]() ;当PQ∥BE时,EP=14﹣x,EQ=x﹣9,此时△PEQ∽△BAE,∴
;当PQ∥BE时,EP=14﹣x,EQ=x﹣9,此时△PEQ∽△BAE,∴![]() ,
,
∴![]() ,解得x=
,解得x=![]() .
.
由题意得x的值为:x=![]() 、
、![]() 或
或![]() .
.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
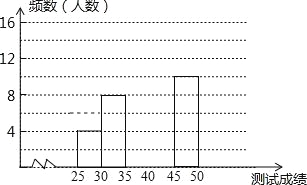
【题目】为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数(人数) |
第1组 | 25≤x<30 | 4 |
第2组 | 30≤x<35 | 8 |
第3组 | 35≤x<40 | 16 |
第4组 | 40≤x<45 | a |
第5组 | 45≤x<50 | 10 |
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
(4)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小宇与小强两名男同学能分在同一组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件为必然事件的是( )
A. 如果a,b是实数,那么ab=ba
B. 抛掷一枚均匀的硬币,落地后正面朝上
C. 汽车行驶到交通岗遇到绿色的信号灯
D. 口袋中装有3个红球,从中随机摸出一球,这个球是白球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将点A(﹣1,﹣2)向右平移4个单位长度得到点B,则点B关于x轴的对称点B′的坐标为( )
A. (﹣5,2) B. (3,2) C. (﹣3,2) D. (3,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于频率和概率的关系,下列说法正确的是
A. 频率等于概率
B. 当实验次数很大时,频率稳定在概率附近
C. 当实验次数很大时,概率稳定在频率附近
D. 实验得到的频率与概率不可能相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形MNPQ中,动点R从点N出发,沿着N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则下列说法不正确的是( )
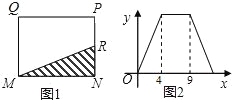
A.当x=2时,y=5
B.矩形MNPQ的面积是20
C.当x=6时,y=10
D.当y=![]() 时,x=10
时,x=10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com