练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】完成下列推理过程

    已知：∠C+∠CBD=180°，∠ABD=85°，∠2=60°，求∠A的度数.

    解：∵∠C+∠CBD=180°（已知）

    ∴DB∥CE（ ）

    ∴∠1＝ ( )

    ∵∠2＝∠3（ ）

    ∴∠1＝∠2=60° ( )

    又∵ ∠ABD=85°（已知）

    ∴∠A＝180°-∠ABD-∠1= （三角形三内角和为180°）

    【答案】同旁内角互补，两直线平行；∠3；两直线平行，同位角相等；对顶角相等；等量代换；35°．

    【解析】

    根据平行线的判定定理和性质定理、三角形内角和定理填空即可．

    解：∵∠C+∠CBD=180°（已知）

    ∴DB∥CE（同旁内角互补，两直线平行）

    ∴∠1＝∠3（两直线平行，同位角相等）

    ∵∠2＝∠3（对顶角相等）

    ∴∠1＝∠2=60°（等量代换）

    又∵ ∠ABD=85°（已知）

    ∴∠A＝180°-∠ABD-∠1=35°（三角形三内角和为180°）

    故答案为：同旁内角互补，两直线平行；∠3；两直线平行，同位角相等；对顶角相等；等量代换；35°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

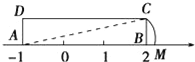
    【题目】如图，矩形ABCD中，AB=3，AD=1，AB在数轴上，若以点A为圆心，对角线AC的长为半径作弧交数轴的正半轴于M，则点M的表示的数为________________．

    【答案】

    【解析】AC＝AM＝＝，∴AM＝

    【题型】填空题
    【结束】
    11

    【题目】在△ABC中，AB＝10，AC＝2，BC边上的高AD＝6，则另一边BC等于_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法中正确的是（　　）.

    A. “打开电视机，正在播放《动物世界》”是必然事件

    B. 某种彩票的中奖概率为，说明每买1000张，一定有一张中奖

    C. 抛掷一枚质地均匀的硬币一次，出现正面朝上的概率为

    D. 想了解长沙市所有城镇居民的人均年收入水平，宜采用抽样调查

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】完成下面的证明：

    已知：如图，点D，E，F分别在线段AB，BC，AC上，连接DE、EF，DM平分∠ADE交EF于点M，∠1+∠2=180°．

    求证： ∠B =∠BED．

    证明：∵∠1+∠2=180°（已知），

    又∵∠1+∠BEM=180°（ ），

    ∴∠2=∠BEM（ 　　），

    ∴DM∥______（_________________________________________）．

    ∴∠ADM =∠B（_________________________________________），

    ∠MDE =∠BED（_______________________________________）．

    又∵DM平分∠ADE (已知)，

    ∴∠ADM =∠MDE ( )．

    ∴∠B =∠BED（等量代换）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一次函数y=x+4的图象与二次函数y=ax（x﹣2）的图象相交于A（﹣1，b）和B，点P是线段AB上的动点（不与A、B重合），过点P作PC⊥x轴，与二次函数y=ax（x﹣2）的图象交于点C．

    （1）求a、b的值
    （2）求线段PC长的最大值；
    （3）若△PAC为直角三角形，请直接写出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面的图象反映的过程是：张强从家跑步去体育场，在那里锻炼了一阵后又原路返回，顺路到文具店去买笔，然后散步回家.其中x表示时间，y表示张强离家的距离.根据图象回答：

    （1）体育场离张强家的多远？张强从家到体育场用了多长时间？

    （2）体育场离文具店多远？

    （3）张强在文具店逗留了多久？

    （4）计算张强从文具店回家的平均速度.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】明的父亲在批发市场按每千克1.8元批发了若干千克的西瓜进城出售,为了方便，他带了一些零钱备用．他先按市场价售出一些后，又降价出售．售出西瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示，结合图像回答下列问题：

    (1)降价前他每千克西瓜出售的价格是多少?

    (2)随后他按每千克下降0.5元将剩余的西瓜售完，这时他手中的钱(含备用的钱)是450元， 问他一共批发了多少千克的西瓜?

    (3)小明的父亲这次一共赚了多少钱?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一枚运载火箭从地面L处发射，当火箭到达A点时，从位于距发射架底部4km处的地面雷达站R（LR=4）测得火箭底部的仰角为43°．1s后，火箭到达B点，此时测得火箭底部的仰角为45.72°．这枚火箭从A到B的平均速度是多少 （结果取小数点后两位）？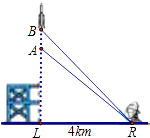

    （参考数据：sin43°≈0.682，cos43°≈0.731，tan43°≈0.933，
    sin45.72°≈0.716，cos45.72°≈0.698，tan45.72°≈1.025）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，AD∥BC，∠BAD=90°，对角线BD⊥DC．

    （1）求证：△ABD∽△DCB；
    （2）如果AD=4，BC=9，求BD的长．

    查看答案和解析>>

    同步练习册答案