
 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=$\frac{k^2}{x}$(x<0,k是不等于0的常数)图象上一点,AO的延长线交函数y=$\frac{1}{x}$(x>0)的图象于点C.点A关于y轴的对称点为A′;点C关于x轴的对称点为C′,关于原点对称点是C′′.连结CC′,交x轴于点B,连结AB,AA′,A′C′,若△ABC的面积等于2,则四边形A A′C′C′′的面积等于( )
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=$\frac{k^2}{x}$(x<0,k是不等于0的常数)图象上一点,AO的延长线交函数y=$\frac{1}{x}$(x>0)的图象于点C.点A关于y轴的对称点为A′;点C关于x轴的对称点为C′,关于原点对称点是C′′.连结CC′,交x轴于点B,连结AB,AA′,A′C′,若△ABC的面积等于2,则四边形A A′C′C′′的面积等于( )| A. | 7 | B. | 8 | C. | 3 | D. | 4 |
分析 延长CC′交AA′于点E,令C′C″、AA′与y轴的交点分别为M、N点,由反比例函数系数k的几何意义可得知S△OBC=$\frac{1}{2}$,结合S△ABC=2以及三角形的面积公式即可得出AE=4OB,即AN=3OB;结合对称点的性质可得出△OC″M∽△OAN,根据相似三角形的性质即可得出$\frac{OM}{ON}=\frac{C″M}{AN}$=$\frac{1}{3}$,由此得出MN=2BC,结合梯形的面积公式以及三角形的面积公式即可得出S梯形AA′C′C″=16S△OBC,由此得出结论.
解答 解:延长CC′交AA′于点E,令C′C″、AA′与y轴的交点分别为M、N点,如图所示.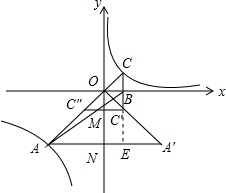
∵S△ABC=$\frac{1}{2}$BC•AE=2,S△OBC=$\frac{1}{2}$BC•OB=$\frac{1}{2}$×|1|=$\frac{1}{2}$,
∴AE=4OB,
又∵OB=NE,
∴AN=3OB.
∵点A关于y轴的对称点为A′;点C关于x轴的对称点为C′,关于原点对称点是C″,
∴BC=BC′,AN=A′N=3OB,C′M=C″M=OB.
∵C″M⊥y轴,AN⊥y轴,
∴C″M∥AN,
∴△OC″M∽△OAN,
∴$\frac{OM}{ON}=\frac{C″M}{AN}$=$\frac{1}{3}$,
∴MN=ON-OM=2OM=2BC.
S梯形AA′C′C″=$\frac{1}{2}$(C′C″+AA′)•MN=$\frac{1}{2}$(2OB+6OB)•2BC=8OB•BC=16•S△OBC=8.
故选B.
点评 本题考查了反比例函数系数k的几何意义、对称点的性质以及三角形(平行四边形)的面积公式,解题的关键是找出S梯形AA′C′C″=16S△OBC.本题属于中档题,难度不大,解决该题型题目时,利用等底三角形的面积公式找出高与高之间的比例,再结合相似三角形的性质得出边的比例关系是关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
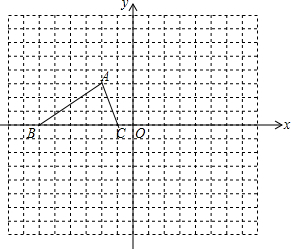 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
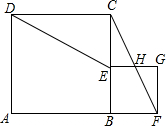 如图,点B在线段AF上,分别以AB、BF为边在线段AF的同侧作正方形ABCD和正方形BFGE,连接CF和DE,CF交EG于H.
如图,点B在线段AF上,分别以AB、BF为边在线段AF的同侧作正方形ABCD和正方形BFGE,连接CF和DE,CF交EG于H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 打开电视机,正在播放广告 | |
| B. | 掷一枚均匀硬币,正面一定朝上 | |
| C. | 每周的星期日一定是晴天 | |
| D. | 我市夏季的平均气温比冬季的平均气温高 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
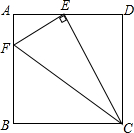 如图,已知E是矩形ABCD边AD的中点,F是AB上一点,EF⊥CE,若AB:BC=$\sqrt{3}$:2,同图中(有4个三角形)相似三角形有3对.
如图,已知E是矩形ABCD边AD的中点,F是AB上一点,EF⊥CE,若AB:BC=$\sqrt{3}$:2,同图中(有4个三角形)相似三角形有3对.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com