
 )2+
)2+ 的形式,并据此说明,当x为何值时,张阿姨出租格子柜的月收益最大?最大的月收益是多少?
的形式,并据此说明,当x为何值时,张阿姨出租格子柜的月收益最大?最大的月收益是多少?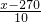 套,
套,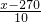 )x-(2x-540)=-
)x-(2x-540)=-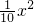 +65x+540;
+65x+540;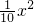 +65x+540,
+65x+540, (x2-2×325x+3252)+540+
(x2-2×325x+3252)+540+ ×3252,
×3252, (x-325)2+11102.5
(x-325)2+11102.5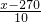 ,所有未出租设备支出的费用为(2x-540)元,依题意可知共收入(40-
,所有未出租设备支出的费用为(2x-540)元,依题意可知共收入(40-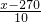 )x,再根据总收益=设备租金收入-未租出格子柜支出费用,即可列出y关于x的函数关系.
)x,再根据总收益=设备租金收入-未租出格子柜支出费用,即可列出y关于x的函数关系.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| b |
| 2a |
| 4ac-b2 |
| 4a |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2011年浙江省杭州市中考数学模拟试卷(24)(解析版) 题型:解答题
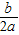 )2+
)2+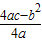 的形式,并据此说明,当x为何值时,张阿姨出租格子柜的月收益最大?最大的月收益是多少?
的形式,并据此说明,当x为何值时,张阿姨出租格子柜的月收益最大?最大的月收益是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com