
 如图,平行四边形ABCD中,∠ABC=75°,AF⊥BC,垂足为F,AF交BD于E,若DE=2AB,求∠AED的度数.
如图,平行四边形ABCD中,∠ABC=75°,AF⊥BC,垂足为F,AF交BD于E,若DE=2AB,求∠AED的度数. 分析 由DE=2AB,可作辅助线:取DE中点M,连接AM,根据平行四边形的对边平行,易得△ADE是直角三角形,由直角三角形斜边上的中线是斜边的一半,即可得△ADM,△AME,△AMB是等腰三角形,想办法证明∠ABE=2∠DBC,即可解决问题.
解答 解:如图,取DE的中点M,连接AM.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DBC=∠ADM,
∵AF⊥BC,
∴AD⊥AF,
∴∠EAD=90°,
∵EM=DM,
∴AM=DM=EM,
∵DE=2AB,
∴AB=AM,
∴∠ABM=∠AMB=∠MAD+∠ADM,
∵MA=MD,
∴∠ADM=∠MAD=∠DBC,
∴∠ABM=∠AMB=2∠ADM=2∠DBC,
∴3∠DBC=75°,
∴∠DBC=25°,
∵∠EFB=90°,
∴∠AED=∠FEB=90°-∠EBF=65°.
点评 此题考查了直角三角形的性质(直角三角形斜边上的中线是斜边的一半)、平行四边形的性质(平行四边形的对边平行)以及等腰三角形的性质(等边对等角),解题的关键是注意方程思想的应用.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:解答题
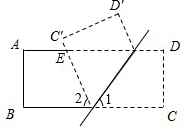 如图,长方形纸片CD沿MN折叠(M,N在AD、BC上),AD∥BC,C′,D′为C、D的对称点,C′N交AD于E.
如图,长方形纸片CD沿MN折叠(M,N在AD、BC上),AD∥BC,C′,D′为C、D的对称点,C′N交AD于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
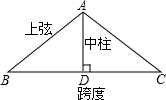 如图,厂房屋顶人字架(等腰三角形)的跨度为20m,∠B=37°,求中柱AD(D为底边中点)和上弦AB的长(参考数据:cos37°≈0.6)
如图,厂房屋顶人字架(等腰三角形)的跨度为20m,∠B=37°,求中柱AD(D为底边中点)和上弦AB的长(参考数据:cos37°≈0.6)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com