
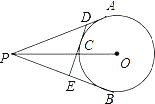
【题目】如图,PA、PB切⊙O于A.B,点C在AB上,DE切⊙O于C,交PA、PB于D.E,已知PO=5cm,⊙O的半径为3cm,则△PDE的周长是______.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】梧桐山是深圳最高的山峰,某校综合实践活动小组要测量“主山峰”的高度,先在梧桐山对面广场的A处测得“峰顶”C的仰角为45°,此时,他们刚好与峰底D在同一水平线上.然后沿着坡度为30°的斜坡正对着“主山峰”前行700米,到达B处,再测得“峰顶”C的仰角为60°,如图,根据以上条件求出“主山峰”的高度?(测角仪的高度忽略不计,结果精确到1米).参考数据:(![]() 1.4,
1.4,![]() 1.7)
1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD,把△BCD沿BD翻折,得△BDG,BG,AD所在的直线交于点E,过点D作DF∥BE交BC所在直线于点F.

(1)求证:四边形DEBF是菱形;
(2)若AB=8,AD=4,求四边形BEDF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
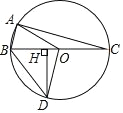
【题目】如图,⊙O 是△ABC 的外接圆,BC 是直径,AC=2DH,过点 D 作 DH 垂直BC 于点 H,以下结论中:①BH=HD;②∠BAO=∠BOD;③![]() ;④连接 AO、BD,若 BC=8,sin∠HDO=
;④连接 AO、BD,若 BC=8,sin∠HDO=![]() ,则四边形 ABDO 的面积为
,则四边形 ABDO 的面积为![]() , 其中正确的结论是 ____(请填写序号)
, 其中正确的结论是 ____(请填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A的坐标为(a,4)(其中a<-3),射线OA与反比例函数![]() 的图象交于点P,点B,C分别在函数
的图象交于点P,点B,C分别在函数![]() 的图象上,且AB∥x轴,AC∥y轴,连结BO,CO,BP,CP.
的图象上,且AB∥x轴,AC∥y轴,连结BO,CO,BP,CP.
(1)当a=-6,求线段AC的长;
(2)当AB=BO时,求点A的坐标;
(3)求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形![]() 是菱形,点
是菱形,点![]() 分别在
分别在![]() 上,且
上,且![]() ,点
,点![]() 分别在
分别在![]() 上,
上,![]() 与
与![]() 相交于点
相交于点![]() .
.
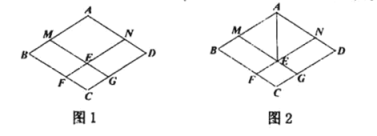
(1)如图1,求证:四边形![]() 是菱形;
是菱形;
(2)如图2,连接![]() ,在不添加任何辅助线的情况下,请直接写出面积相等的四边形
,在不添加任何辅助线的情况下,请直接写出面积相等的四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
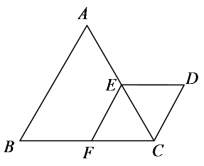
【题目】如图,△ABC与△CDE都是等边三角形,点E、F分别在AC、BC上,且EF∥AB.
(1)求证:四边形EFCD是菱形;
(2)设CD=2,求D、F两点间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“过一点作已知直线的垂线”的尺规作图过程,请你阅读后完成相应任务,如图,已知直线![]() 及上一点
及上一点![]() .求作:直线
.求作:直线![]() ,使
,使![]() 于点
于点![]() .
.
作法:①在直线![]() 外任取一点
外任取一点![]() ;②以点
;②以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交直线
长为半径画弧,交直线![]() 于点
于点![]() (不与点
(不与点![]() 重合)③作射线
重合)③作射线![]() ,交①中所画的弧于点
,交①中所画的弧于点![]() ;④作直线
;④作直线![]() ,直线
,直线![]() 就是所求作的直线
就是所求作的直线![]() 的垂线.
的垂线.
任务:(1)根据小明设计的尺规作图过程,补全图形(要求:尺规作图,保留作图痕迹);
(2)证明上述方法得到的直线![]() 直线
直线![]() .
.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com