
 .设梯形的面积为S,梯形中较短的底的长为x,试写出梯形面积S关于x的函数关系式,并指出自变量x的取值范围.
.设梯形的面积为S,梯形中较短的底的长为x,试写出梯形面积S关于x的函数关系式,并指出自变量x的取值范围. 时,设BE=m,表示出AB,再根据矩形的周长列式表示出m,然后根据梯形的面积公式列式整理即可得解,再根据BE与BC的长度范围求出x的取值范围;②AE与较长的边的夹角的正切值等于
时,设BE=m,表示出AB,再根据矩形的周长列式表示出m,然后根据梯形的面积公式列式整理即可得解,再根据BE与BC的长度范围求出x的取值范围;②AE与较长的边的夹角的正切值等于 时,设AB=CD=n,表示出BE,然后根据矩形的周长表示出m,再根据矩形的面积公式列式整理即可得解,再根据BE、BC的长度范围求出x的取值范围.
时,设AB=CD=n,表示出BE,然后根据矩形的周长表示出m,再根据矩形的面积公式列式整理即可得解,再根据BE、BC的长度范围求出x的取值范围. 时,设CE=x,BE=m,
时,设CE=x,BE=m,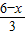 ,
, (AD+EC)•DC,
(AD+EC)•DC, [(m+x)+x]•2m,
[(m+x)+x]•2m,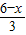 •
•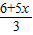 ,
, x2+
x2+ x+4,
x+4,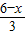 >0,
>0,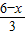 +x>4,
+x>4,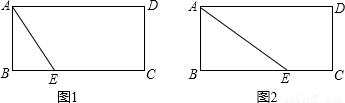
 时,
时,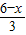 ,
, (AD+EC)•DC,
(AD+EC)•DC, [(2n+x)+x]•n,
[(2n+x)+x]•n,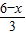 •
•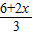 ,
, x2+
x2+ x+4,
x+4,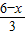 >0,2×
>0,2×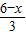 +x>4,
+x>4,

 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源:中考备考专家数学(第二版) 题型:044
已知矩形的长大于宽的2倍,周长为12,从它的一个顶点作一条射线,将矩形分成一个三角形和一个梯形,且这条射线与矩形一边所成的角的正切值等于![]() .设梯形的面积为S,梯形中较短的底的长为x,试写出梯形面积S关于x的函数关系式,并指出自变量x的取值范围.
.设梯形的面积为S,梯形中较短的底的长为x,试写出梯形面积S关于x的函数关系式,并指出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 .设梯形的面积为S,梯形中较短的底的长为x,试写出梯形面积S关于x的函数关系式,并指出自变量x的取值范围.
.设梯形的面积为S,梯形中较短的底的长为x,试写出梯形面积S关于x的函数关系式,并指出自变量x的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com