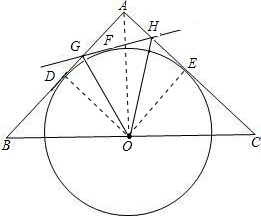
解:(1)连接OD、OE、OA,
∵O是BC边上的点且⊙O与AB、AC都相切,
∴OD⊥AB,AC⊥OE,
又∵∠BAC=90°,且OD=OE,
∴四边形ADOE为正方形,
∴OE=AE,
∴∠OAE=45°;
又∵∠C=45°,
∴OE=2,△OAC为等腰直角三角形,
AE=EC=

AC=

×4=2,即⊙O的半径是2;

(2)②的结论正确;理由如下:
连接OF、OG、OH,
由题意,GD、GF以及HF、HE与圆相切,
所以GD=GF,HE=HF,∠DOG=∠FOG,∠FOH=∠HOE,
而∠DOE=90°,所以可以得到∠GOH=

=45°.
(3)BG=x,CH=y,
易得:GF=GD=x-2,FH=HE=y-2,AG=4-x,AE=4-y,
所以GH=x+x-4,
由∠A=90°,可得GH
2=AG
2+AH
2,代入上述各数值,
化简可得y=

,由AG≥0,AE≥0,可得x≤0,y≤4,所以2≤x≤4,
当x=y时,有AG=AH,由于AB=AC所以可得GH与BC平行,连接AO,
设AO交GH于F',有∠OFH=90°,
所以F'为切点F,即F为AO与圆的交点同时F是

的中点.
分析:(1)连接OD、OE、OA;构造正方形和直角三角形,利用勾股定理和正方形的性质解答;
(2)连接OF、OG、OH;根据切线长定理和圆的半径相等,构造全等三角形,即△DOG≌△FOG,△FOH≌△EOH;得到相等的角∠DOG=∠FOG,∠FOH=∠EOH;进而得到∠GOH=

=45°;
(3)当x=y时,有AG=AH,根据平行线分线段成比例定理的逆定理,判定GH∥BC,根据切线性质,判断F为AO与圆的交点同时F是

的中点.
点评:本题是一道关于圆的综合题,考查了切线的性质、和圆相关的正方形的性质、切线长定理以及结合切线长定理的点的存在性问题,范围较广,有一定的开放性,有利于培养同学们的发散思维能力.

 上的一个动点(不与D、E),过点F作⊙O的切线分别与边AB、AC相交于G、H,连接OG、OH,有两个结论:①四边形BCHG的周长不变,②∠GOH的度数不变.已知这两个结论只有一个正确,找出正确的结论并证明;
上的一个动点(不与D、E),过点F作⊙O的切线分别与边AB、AC相交于G、H,连接OG、OH,有两个结论:①四边形BCHG的周长不变,②∠GOH的度数不变.已知这两个结论只有一个正确,找出正确的结论并证明;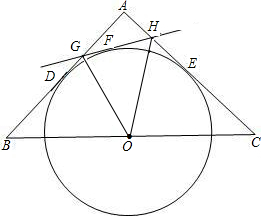 的函数关系,写出你的探究过程并确定自变量x的取值范围,并说明当x=y时F点的位置.
的函数关系,写出你的探究过程并确定自变量x的取值范围,并说明当x=y时F点的位置. 解:(1)连接OD、OE、OA,
解:(1)连接OD、OE、OA, AC=
AC= ×4=2,即⊙O的半径是2;
×4=2,即⊙O的半径是2;
 =45°.
=45°. ,由AG≥0,AE≥0,可得x≤0,y≤4,所以2≤x≤4,
,由AG≥0,AE≥0,可得x≤0,y≤4,所以2≤x≤4, 的中点.
的中点. =45°;
=45°; 的中点.
的中点.
