
 在正△ABC内有一点P,PA=2,PB=2$\sqrt{3}$,PC=4,则CB的长为2$\sqrt{7}$.
在正△ABC内有一点P,PA=2,PB=2$\sqrt{3}$,PC=4,则CB的长为2$\sqrt{7}$. 分析 先把△ABP绕点A逆时针旋转60°可得到△CBD,如图,则利用旋转的性质得BD=BP=2$\sqrt{3}$,∠PBD=60°,CD=AP=2,于是可判断△PBD为等边三角形,从而得到PD=PB=2$\sqrt{3}$,∠PDB=60°,再利用勾股定理的逆定理可证明∠PDC=90°,作BH⊥CD于H,如图,则∠BDH=30°,在Rt△BDH中利用含30度的直角三角形三边的关系计算出BH=$\frac{1}{2}$BD=$\sqrt{3}$,DH=$\sqrt{3}$BH=3,则CH=CD+DH=5,然后在Rt△BCH中根据勾股定理可计算出BC.
解答 解:∵△ABC为等边三角形,
∴BA=BC,∠ABC=60°,
∴把△ABP绕点A逆时针旋转60°可得到△CBD,如图,
∴BD=BP=2$\sqrt{3}$,∠PBD=60°,CD=AP=2,
∴△PBD为等边三角形,
∴PD=PB=2$\sqrt{3}$,∠PDB=60°,
在△PCD中,∵PC=2,PD=2$\sqrt{3}$,PC=4,
而22+(2$\sqrt{3}$)2=42,
∴PC2+PD2=PC2,
∴△PCD为直角三角形,∠PDC=90°,
∴∠BDC=60°+90°=150°,
作BH⊥CD于H,如图,∵∠BDH=180°-∠BDC=30°,
∴BH=$\frac{1}{2}$BD=$\sqrt{3}$,DH=$\sqrt{3}$BH=3,
∴CH=CD+DH=2+3=5,
在Rt△BCH中,BC=$\sqrt{B{H}^{2}+C{H}^{2}}$=$\sqrt{(\sqrt{3})^{2}+{5}^{2}}$=2$\sqrt{7}$.
故答案为2$\sqrt{7}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.解决本题的关键是利用旋转由三条已知线段构成一个直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | -(-2)2=4 | B. | -[-(5)]=5 | C. | $\frac{2^2}{3}=\frac{4}{9}$ | D. | ${({-3})^2}×({-\frac{1}{3}})=3$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 近似数6.91精确到十分位 | |
| B. | 将数80 360用科学计数法表示为80.36×103 | |
| C. | 用四舍五入法得到的近似数17.8350精确到0.001 | |
| D. | 用科学计数法表示的数6.06×104,其原数为60 600 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
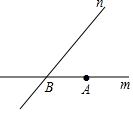 如图,直线m,n交于点B,m、n的夹角为50°,点A是直线m上的点,在直线n上寻找一点C,使△ABC是等腰三角形,这样的C点有多少个?( )
如图,直线m,n交于点B,m、n的夹角为50°,点A是直线m上的点,在直线n上寻找一点C,使△ABC是等腰三角形,这样的C点有多少个?( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 重庆一中研究性学习小组准备利用所学的三角函数的知识取测量南山大金鹰的高度.他们在B处测得山顶C的仰角是45°,从B沿坡度为1:$\sqrt{3}$的斜度前进38米到达大金鹰上的一个观景点D,再次测得山顶C的仰角为60°,则大金鹰的高度AC为( )米(结果精确到1米.参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
重庆一中研究性学习小组准备利用所学的三角函数的知识取测量南山大金鹰的高度.他们在B处测得山顶C的仰角是45°,从B沿坡度为1:$\sqrt{3}$的斜度前进38米到达大金鹰上的一个观景点D,再次测得山顶C的仰角为60°,则大金鹰的高度AC为( )米(结果精确到1米.参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)| A. | 45 | B. | 48 | C. | 52 | D. | 54 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 信件质量/克 | 0<m≤20 | 20<m≤40 | 40<m≤60 |
| 邮费/元 | 0.80 | 1.20 | 1.60 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 作A关于l的对称点A′,连接A′B交l与P | |
| B. | AB的延长线与l交于P | |
| C. | 作A关于l的对称点A′,连接AA′交l与P | |
| D. | 以上都不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com