
”¾ĢāÄæ”æŅŃÖŖ¶ąĻīŹ½x3©3xy2©4µÄ³£ŹżŹĒa£¬“ĪŹżŹĒb£®
£Ø1£©Ōņa=_____£¬b=_____£»²¢½«ÕāĮ½ŹżŌŚŹżÖįÉĻĖł¶ŌÓ¦µÄµćA”¢B±ķŹ¾³öĄ“£»
£Ø2£©ŹżÖįÉĻŌŚBµćÓŅ±ßÓŠŅ»µćCµ½A”¢BĮ½µćµÄ¾ąĄėÖ®ŗĶĪŖ11£¬ĒóµćCŌŚŹżÖįÉĻĖł¶ŌÓ¦µÄŹż£»
£Ø3£©ŌŚŹżÖįÉĻŹĒ·ń“ęŌŚµćP£¬Ź¹Pµ½A”¢B”¢CµÄ¾ąĄėŗĶµČÓŚ12£æČō“ęŌŚ£¬ĒóµćP¶ŌÓ¦µÄŹż£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
£Ø4£©ŌŚŹżÖįÉĻŹĒ·ń“ęŌŚµćP£¬Ź¹Pµ½A”¢B”¢CµÄ¾ąĄėŗĶ×īŠ”£æČō“ęŌŚ£¬ĒóøĆ×īŠ”Öµ£¬²¢Ēó“ĖŹ±Pµć¶ŌÓ¦µÄŹż£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
![]()
”¾“š°ø”æ(1)-4£¬3£»£Ø2£©5£»£Ø3£©P=0»ņ![]() £»£Ø4£©µćP±ķŹ¾µÄŹżĪŖ3Ź±£¬Pµ½A”¢B”¢CµÄ¾ąĄėŗĶ×īŠ”£¬×īŠ”ÖµĪŖ9£®
£»£Ø4£©µćP±ķŹ¾µÄŹżĪŖ3Ź±£¬Pµ½A”¢B”¢CµÄ¾ąĄėŗĶ×īŠ”£¬×īŠ”ÖµĪŖ9£®
”¾½āĪö”æ£Ø1£©øł¾Ż¶ąĻīŹ½ÖŠ³£ŹżĻī¼°¶ąĻīŹ½µÄ“ĪŹżµÄ¶ØŅ弓æÉĒó½ā£»
£Ø2£©ÉčµćCŌŚŹżÖįÉĻĖł¶ŌÓ¦µÄŹżĪŖx£¬øł¾ŻCA+CB=11ĮŠ³ö·½³Ģ£¬½ā·½³Ģ¼“æÉ£»
£Ø3£©ÉčµćPŌŚŹżÖįÉĻĖł¶ŌÓ¦µÄŹżĪŖa£¬Ōņ|a+4|+|a-3|+|a-5|=12£¬øł¾Ż¾ų¶ŌÖµµÄŠŌÖŹĒó½āæÉµĆ£»
£Ø4£©µćPŌŚµćAŗĶµćB£Øŗ¬µćAŗĶµćB£©Ö®¼ä£¬ŅĄ“Ė¼“æÉĒó½ā£®
£Ø1£©”߶ąĻīŹ½x3-3xy2-4µÄ³£ŹżĻīŹĒa£¬“ĪŹżŹĒb£¬
”ąa=-4£¬b=3£¬
µćA”¢BŌŚŹżÖįÉĻČēĶ¼ĖłŹ¾£ŗ
![]() £¬
£¬
¹Ź“š°øĪŖ£ŗ-4”¢3£»
£Ø2£©ÉčµćCŌŚŹżÖįÉĻĖł¶ŌÓ¦µÄŹżĪŖx£¬
”ßCŌŚBµćÓŅ±ß£¬
”ąx£¾3£®
øł¾ŻĢāŅāµĆ
x-3+x-£Ø-4£©=11£¬
½āµĆx=5£¬
¼“µćCŌŚŹżÖįÉĻĖł¶ŌÓ¦µÄŹżĪŖ5£»
£Ø3£©ÉčµćPŌŚŹżÖįÉĻĖł¶ŌÓ¦µÄŹżĪŖa£¬
Ōņ|a+4|+|a-3|+|a-5|=12£¬
1”ć”¢µ±a£¼-4Ź±£¬-a-4+3-a+5-a=12£¬½āµĆa=-![]() £¾-4£ØÉį£©£»
£¾-4£ØÉį£©£»
2”ć”¢µ±-4”Üa£¼3Ź±£¬a+4+a-3+5-a=12£¬½āµĆa=0£»
3”ć”¢µ±3”Üa£¼5Ź±£¬a+4+a-3+5-a=12£¬½āµĆa=6£¾5£ØÉį£©£»
4”ć”¢µ±a”Ż5Ź±£¬a+4+a-3+a-5=12£¬½āµĆa=![]() £»
£»
×ŪÉĻ£¬P=0»ņ![]() £»
£»
£Ø4£©“ęŌŚ£¬µćP±ķŹ¾µÄŹżĪŖ3£¬øĆ×īŠ”ÖµĪŖ9£¬
ÉčPµ½A”¢B”¢CµÄ¾ąĄėŗĶĪŖd£¬
Ōņd=|x+4|+|x-3|+|x-5|£¬
1”ćµ±x”Ü-4Ź±£¬d=-x-4+3-x+5-x=-3x+4£¬
x=-4Ź±£¬d×īŠ”=16£»
2”ć”¢µ±-4£¼x”Ü3Ź±£¬d=x+4+3-x+5-x=-x+12£¬
x=3Ź±£¬d×īŠ”=9£»
3”ć”¢µ±3£¼x”Ü5Ź±£¬d=x+4+x-3+5-x=x+6£¬
x=5Ź±£¬d×īŠ”=11£»
4”ć”¢µ±x£¾5Ź±£¬d=x+4+x-3+x-5=3x-4£¬“ĖŹ±ĪŽ×īŠ”Öµ£»
×ŪÉĻ£¬µ±µćP±ķŹ¾µÄŹżĪŖ3Ź±£¬Pµ½A”¢B”¢CµÄ¾ąĄėŗĶ×īŠ”£¬×īŠ”ÖµĪŖ9£®


 Ģ½¾æÓė¹®¹ĢŗÓÄĻæĘѧ¼¼Źõ³ö°ęÉēĻµĮŠ“š°ø
Ģ½¾æÓė¹®¹ĢŗÓÄĻæĘѧ¼¼Źõ³ö°ęÉēĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ÓŠĮ½Ģõ¹«Ā·OM”¢ONĻą½»³É30”ć½Ē£¬ŃŲ¹«Ā·OM·½ĻņĄėOµć80Ćד¦ÓŠŅ»ĖłŃ§Š£A£®µ±ÖŲŠĶŌĖŹäæسµPŃŲµĄĀ·ON·½ĻņŠŠŹ»Ź±£¬ŌŚŅŌPĪŖŌ²ŠÄ50Ć׳¤ĪŖ°ė¾¶µÄŌ²ŠĪĒųÓņÄŚ¶¼»įŹÜµ½æسµŌėÉłµÄÓ°Ļģ£¬ĒŅæسµPÓėѧŠ£AµÄ¾ąĄėŌ½½üŌėÉłÓ°ĻģŌ½“ó£®ČōŅ»Ö±ÖŲŠĶŌĖŹäæسµPŃŲµĄĀ·ON·½ĻņŠŠŹ»µÄĖŁ¶ČĪŖ18Ē§Ć×/Ź±£®

£Ø1£©Ēó¶ŌѧŠ£AµÄŌėÉłÓ°Ļģ×ī“óŹ±æسµPÓėѧŠ£AµÄ¾ąĄė£»
£Ø2£©ĒóæسµPŃŲµĄĀ·ON·½ĻņŠŠŹ»Ņ»“ĪøųѧŠ£A“ųĄ“ŌėÉłÓ°ĻģµÄŹ±¼ä£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ö±ĻßABŗĶCDĻą½»ÓŚµćO£¬”ĻCOE£½90”ć£¬ODĘ½·Ö”ĻBOF£¬”ĻBOE£½50”ć.
(1)Ēó”ĻAOCµÄ¶ČŹż£»
(2)Ēó”ĻEOFµÄ¶ČŹż£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĖıߊĪ![]() ÖŠ£¬
ÖŠ£¬ ![]() £¬
£¬ ![]() ”¢
”¢![]() ·Ö±šŹĒ
·Ö±šŹĒ![]() ”¢
”¢![]() µÄÖŠµć£®
µÄÖŠµć£®

£Ø![]() £©ĒóÖ¤£ŗ
£©ĒóÖ¤£ŗ ![]() £®
£®
£Ø![]() £©Čō
£©Čō![]() £¬Ēó
£¬Ēó![]() µÄ¶ČŹż£®
µÄ¶ČŹż£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬¾ŲŠĪOABCµÄ±ßOA£¬OC·Ö±šŌŚxÖį”¢yÖįÉĻ£¬µćBŌŚµŚŅ»ĻóĻŽ£¬µćDŌŚ±ßBCÉĻ£¬ĒŅ”ĻAOD=30”ć£¬ĖıߊĪOA”äB”äDÓėĖıߊĪOABD¹ŲÓŚÖ±ĻßOD¶Ō³Ę£ØµćA”äŗĶA£¬B”äŗĶB·Ö±š¶ŌÓ¦£©£®ČōAB=1£¬·“±ČĄżŗÆŹży= ![]() £Øk”Ł0£©µÄĶ¼ĻóĒ”ŗĆ¾¹żµćA”䣬B£¬ŌņkµÄÖµĪŖ £®
£Øk”Ł0£©µÄĶ¼ĻóĒ”ŗĆ¾¹żµćA”䣬B£¬ŌņkµÄÖµĪŖ £® 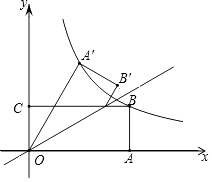
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ£¼Ę»®×éÖÆŹ¦Éś¹²300ČĖ²Ī¼ÓŅ»“Ī“óŠĶ¹«Ņę»ī¶Æ£¬Čē¹ū×āÓĆ6Į¾“óæĶ³µŗĶ5Į¾Š”æĶ³µĒ”ŗĆČ«²æ×ųĀś£¬ŅŃÖŖĆæĮ¾“óæĶ³µµÄ³ĖæĶ׳Ī»Źż±ČŠ”æĶ³µ¶ą17øö.
(1)ĒóĆæĮ¾“óæĶ³µŗĶĆæĮ¾Š”æĶ³µµÄ³ĖæĶ׳Ī»Źż£»
(2)ÓÉÓŚ×īŗó²Ī¼Ó»ī¶ÆµÄČĖŹżŌö¼ÓĮĖ30ČĖ£¬Ń§Š£¾ö¶Øµ÷Õū×ā³µ·½°ø£¬ŌŚ±£³Ö×āÓĆ³µĮ¾×ÜŹż²»±äµÄĒéæöĻĀ£¬ĪŖ½«ĖłÓŠ²Ī¼Ó»ī¶ÆµÄŹ¦Éś×°ŌŲĶź³É£¬Ēó×āÓĆŠ”æĶ³µŹżĮæµÄ×ī“óÖµ.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£Ø1£©£¬Rt”÷AOBÖŠ£¬”ĻA=90”ć£¬”ĻAOB=60”ć£¬OB=![]() £¬”ĻAOBµÄĘ½·ÖĻßOC½»ABÓŚC£¬¹żOµć×öÓėOB“¹Ö±µÄÖ±ĻßON£®¶ÆµćP“ÓµćB³ö·¢ŃŲÕŪĻßBC©COŅŌĆæĆė1øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņÖÕµćOŌĖ¶Æ£¬ŌĖ¶ÆŹ±¼äĪŖtĆė£¬Ķ¬Ź±¶ÆµćQ“ÓµćC³ö·¢ŃŲÕŪĻßCO©ONŅŌĻąĶ¬µÄĖŁ¶ČŌĖ¶Æ£¬µ±µćPµ½“ļµćOŹ±P”¢QĶ¬Ź±Ķ£Ö¹ŌĖ¶Æ£®
£¬”ĻAOBµÄĘ½·ÖĻßOC½»ABÓŚC£¬¹żOµć×öÓėOB“¹Ö±µÄÖ±ĻßON£®¶ÆµćP“ÓµćB³ö·¢ŃŲÕŪĻßBC©COŅŌĆæĆė1øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņÖÕµćOŌĖ¶Æ£¬ŌĖ¶ÆŹ±¼äĪŖtĆė£¬Ķ¬Ź±¶ÆµćQ“ÓµćC³ö·¢ŃŲÕŪĻßCO©ONŅŌĻąĶ¬µÄĖŁ¶ČŌĖ¶Æ£¬µ±µćPµ½“ļµćOŹ±P”¢QĶ¬Ź±Ķ£Ö¹ŌĖ¶Æ£®
£Ø1£©ĒóOC”¢BCµÄ³¤£»
£Ø2£©Éč”÷CPQµÄĆ껿ĪŖS£¬ĒóSÓėtµÄŗÆŹż¹ŲĻµŹ½£»
£Ø3£©µ±PŌŚOCÉĻQŌŚONÉĻŌĖ¶ÆŹ±£¬ČēĶ¼£Ø2£©£¬ÉčPQÓėOA½»ÓŚµćM£¬µ±tĪŖŗĪÖµŹ±£¬”÷OPMĪŖµČŃüČż½ĒŠĪ£æĒó³öĖłÓŠĀś×ćĢõ¼žµÄtÖµ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”湫ŌŖĒ°5ŹĄ¼Ķ£¬±Ļ“ļøēĄĖ¹Ń§ÅÉÖŠµÄŅ»Ćū³ÉŌ±Ļ£²®Ė÷Ė¹·¢ĻÖĮĖĪŽĄķŹż ![]() £¬µ¼ÖĀĮĖµŚŅ»“ĪŹżŃ§Ī£»ś£¬
£¬µ¼ÖĀĮĖµŚŅ»“ĪŹżŃ§Ī£»ś£¬ ![]() ŹĒĪŽĄķŹżµÄÖ¤Ć÷ČēĻĀ£ŗ ¼ŁÉč
ŹĒĪŽĄķŹżµÄÖ¤Ć÷ČēĻĀ£ŗ ¼ŁÉč ![]() ŹĒÓŠĄķŹż£¬ÄĒĆ“ĖüæÉŅŌ±ķŹ¾³É
ŹĒÓŠĄķŹż£¬ÄĒĆ“ĖüæÉŅŌ±ķŹ¾³É ![]() £ØpÓėqŹĒ»„ÖŹµÄĮ½øöÕżÕūŹż£©£®ÓŚŹĒ£Ø
£ØpÓėqŹĒ»„ÖŹµÄĮ½øöÕżÕūŹż£©£®ÓŚŹĒ£Ø ![]() £©2=£Ø
£©2=£Ø ![]() £©2=2£¬ĖłŅŌ£¬q2=2p2 £® ÓŚŹĒq2ŹĒżŹż£¬½ų¶ųqŹĒżŹż£¬“Ó¶ųæÉÉčq=2m£¬ĖłŅŌ£Ø2m£©2=2p2 £¬ p2=2m2 £¬ ÓŚŹĒæɵĆpŅ²ŹĒżŹż£®ÕāÓė”°pÓėqŹĒ»„ÖŹµÄĮ½øöÕżÕūŹż”±Ć¬¶Ü£®“Ó¶ųæÉÖŖ”°
£©2=2£¬ĖłŅŌ£¬q2=2p2 £® ÓŚŹĒq2ŹĒżŹż£¬½ų¶ųqŹĒżŹż£¬“Ó¶ųæÉÉčq=2m£¬ĖłŅŌ£Ø2m£©2=2p2 £¬ p2=2m2 £¬ ÓŚŹĒæɵĆpŅ²ŹĒżŹż£®ÕāÓė”°pÓėqŹĒ»„ÖŹµÄĮ½øöÕżÕūŹż”±Ć¬¶Ü£®“Ó¶ųæÉÖŖ”° ![]() ŹĒÓŠĄķŹż”±µÄ¼ŁÉč²»³ÉĮ¢£¬ĖłŅŌ£¬
ŹĒÓŠĄķŹż”±µÄ¼ŁÉč²»³ÉĮ¢£¬ĖłŅŌ£¬ ![]() ŹĒĪŽĄķŹż£®
ŹĒĪŽĄķŹż£®
ÕāÖÖÖ¤Ć÷”° ![]() ŹĒĪŽĄķŹż”±µÄ·½·ØŹĒ£Ø £©
ŹĒĪŽĄķŹż”±µÄ·½·ØŹĒ£Ø £©
A.×ŪŗĻ·Ø
B.·“Ö¤·Ø
C.¾Ł·“Ąż·Ø
D.ŹżŃ§¹éÄÉ·Ø
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø1£©Ģ½¾æÖ¤Ć÷£ŗ
ŌŚ”÷ABCÖŠ£¬”ĻACB=90”ć£¬AC=BC£¬Ö±ĻßMN¾¹żµćC£¬ĒŅAD”ĶMNÓŚµćD£¬BE”ĶMNÓŚµćE£¬µ±Ö±ĻßMNČʵćCŠż×Ŗµ½Ķ¼1µÄĪ»ÖĆŹ±£¬ĒóÖ¤£ŗDE=AD+BE£»
£Ø2£©·¢ĻÖĢ½¾æ£ŗ
µ±Ö±ĻßMNČʵćCŠż×Ŗµ½Ķ¼2µÄĪ»ÖĆŹ±£¬£Ø1£©ÖŠµÄ½įĀŪŹĒ·ń³ÉĮ¢£¬Čē¹ū²»³ÉĮ¢£¬DE”¢AD”¢BEÓ¦Āś×ćµÄ¹ŲĻµŹĒ_____£®
£Ø3£©½ā¾öĪŹĢā£ŗ
µ±Ö±ĻßMNČʵćCŠż×Ŗµ½Ķ¼3µÄĪ»ÖĆŹ±£¬ČōBE=8£¬AD=2£¬ĒėÖ±½ÓŠ“³öDEµÄ³¤ĪŖ_____£®

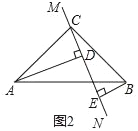
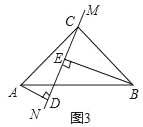
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com