
分析 (1)根据众数和中位数的概念求解;
(2)①用喜欢的40人除以其所占的百分比即可确定总人数;
②首先求得C类所占的百分比,然后用样本容量乘以其所占的百分比即可确定C错误;
③用总数乘以D类所占的百分比就可以确定D类的人数,从而补全统计图即可;
④由抽取人数10除以喜欢的学生数40即可.
解答 解:(1)这组数据按照从小到大的顺序排列为:5,5,6,7,8,8,8,
则众数为:8,
中位数为:7.
故答案为:8,7;
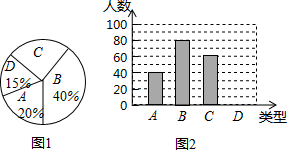
(2)①由条形统计图知A类40人,由扇形统计图知它占抽查人数的20%,∴此次调查的样本容量为:40÷20%=200,故答案为:200;
②C类所占的百分比为:1-40%-20%-15%=25%,
所以C类共有200×25%=50人,
∴C错误,
故答案为C;
③D类的共有200×15%=30人,
正确的条形统计图为:
④200人中喜欢撕名牌游戏的学生40人,抽取10人的概率为:10÷40=$\frac{1}{4}$.
点评 本题考查的是概率,条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:解答题
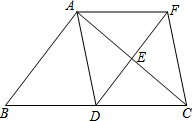 如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接AD、CF.
如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接AD、CF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{10}{3}$a>-$\frac{10}{3}$b | B. | a2>b2 | C. | $\frac{3}{a}$>$\frac{3}{b}$ | D. | -$\frac{1}{5}$+a>-$\frac{1}{5}$+b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{a}{2{b}^{2}}}$=$\frac{1}{2b}$$\sqrt{a}$(b>0) | B. | $\sqrt{\frac{7x}{12{y}^{3}}}$=$\frac{1}{6{y}^{2}}$$\sqrt{21xy}$ | ||
| C. | $\sqrt{{a}^{2}+{b}^{2}}$=a+b(a≥0,b≥0) | D. | 5$\sqrt{\frac{2a}{5}}$=$\sqrt{2a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
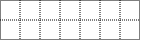 如图是小明家沙发坐垫的平面示意图,中间的双人沙发坐垫面积为2×3(单位面积),左右两边的是坐垫面积为2×2(单位面积)的单人沙发,小明和小虎在玩“藏密码”的游戏,已知小虎将密码藏在沙发坐垫下,则密码藏在单人沙发坐垫下的概率是( )
如图是小明家沙发坐垫的平面示意图,中间的双人沙发坐垫面积为2×3(单位面积),左右两边的是坐垫面积为2×2(单位面积)的单人沙发,小明和小虎在玩“藏密码”的游戏,已知小虎将密码藏在沙发坐垫下,则密码藏在单人沙发坐垫下的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
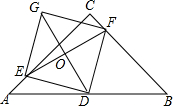 如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=4,D是AB的中点,E,F分别是AC,BC上的点(点E不与端点A,C重合),且AE=CF,连接EF并取EF的中点O,连接DO并延长至点G,使GO=OD,连接DE,DF,GE,GF.
如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=4,D是AB的中点,E,F分别是AC,BC上的点(点E不与端点A,C重合),且AE=CF,连接EF并取EF的中点O,连接DO并延长至点G,使GO=OD,连接DE,DF,GE,GF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com