
【题目】在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.
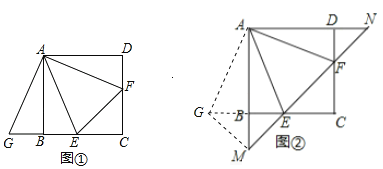
(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;
(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:![]() ;
;
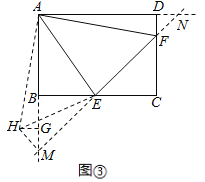
(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.

【答案】(1)证明见试题解析;(2)证明见试题解析;(3)![]() .
.
【解析】
试题分析:(1)由旋转的性质可知AF=AG,∠EAF=∠GAE=45°,即可得到△AEG≌△AEF;
(2)将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.由(1)知△AEG≌△AEF,则有EG=EF.再由△BME、△DNF、△CEF均为等腰直角三角形,得出CE=CF,BE=BM,NF=![]() DF,再证明∠GME=90°,MG=NF,由勾股定理得到
DF,再证明∠GME=90°,MG=NF,由勾股定理得到![]() ,等量代换即可得到
,等量代换即可得到![]() ;
;
(3)延长EF交AB延长线于M点,交AD延长线于N点,将△ADF绕着点A顺时针旋转90°,得到△AGH,连结HM,HE.由(1)知△AEH≌△AEF,得到EF=HE,DF=GH,BE=BM,由(2)知HM⊥ME,得到![]() ,
,![]() ,
,![]() ,从而得到结论.
,从而得到结论.
试题解析:(1)∵△ADF绕着点A顺时针旋转90°,得到△ABG,∴AF=AG,∠FAG=90°,∵∠EAF=45°,∴∠GAE=45°,在△AGE与△AFE中,∵AG=AF,∠GAE=∠FAE=45°,AE=AE,∴△AGE≌△AFE(SAS);
(2)设正方形ABCD的边长为a.将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.则△ADF≌△ABG,DF=BG,由(1)知△AEG≌△AEF,∴EG=EF,∵∠CEF=45°,∴△BME、△DNF、△CEF均为等腰直角三角形,∴CE=CF,BE=BM,NF=![]() DF,∴a﹣BE=a﹣DF,∴BE=DF,∴BE=BM=DF=BG,∴∠BMG=45°,∴∠GME=45°+45°=90°,∴
DF,∴a﹣BE=a﹣DF,∴BE=DF,∴BE=BM=DF=BG,∴∠BMG=45°,∴∠GME=45°+45°=90°,∴![]() ,∵EG=EF,MG=
,∵EG=EF,MG=![]() BM=
BM=![]() DF=NF,∴
DF=NF,∴![]() ;
;
(3)![]() .证明如下:
.证明如下:
如图3所示,延长EF交AB延长线于M点,交AD延长线于N点,将△ADF绕着点A顺时针旋转90°,得到△AGH,连结HM,HE.由(1)知△AEH≌△AEF,∴EF=HE,DF=GH,BE=BM,由(2)知HM⊥ME,∴![]() ,
,![]() ,
,![]() ,∴
,∴![]() .
.


科目:初中数学 来源: 题型:
【题目】某批发商欲将一批水果由A地运往B地,汽车货运公司和铁路货运公司均开办此项运输业务,设运输过程中的损耗均为200元每小时,两货运公司的收费项:目及收费标准如下表所示:
运输工具 | 途中平均速度 | 运费 | 装卸费用 |
汽车 | 80 | 20 | 900 |
火车 | 100 | 15 | 2000 |
(1)设该两地间的距离为x千米,若汽车货运公司和铁路货运公司的总费用分别为y1(元)和y2(元),则y1=元,y2=元;(用含x的代数式表示y1和y2)
(2)如果汽车的总费用比火车的总费用多ll00元,求A,B两地的距离为多少千米?
(3)若两地间距离为200千米,且火车、汽车在路上耽误的时间分别为2小时和3.1小时,若你是经理,选择哪种运输方式更合算些?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,老师要求同学们判断一个四边形的门框是否为矩形,下面是某合作学习小组的四位同学拟定的方案,其中正确的是( )
A. 测量对角线是否相互平分 B. 测量两组对边是否分别相等
C. 测量一组对角线是否垂直 D. 测量其内角是否有三个直角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于体育选考项目统计图
项目 | 频数 | 频率 |
A | 80 | b |
B | c | 0.3 |
C | 20 | 0.1 |
D | 40 | 0.2 |
合计 | a | 1 |
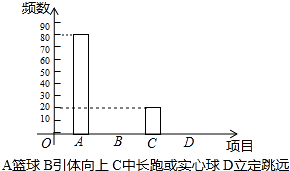
(1)求出表中a,b,c的值,并将条形统计图补充完整. 表中a= , b= , c= .
(2)如果有3万人参加体育选考,会有多少人选择篮球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com