Question

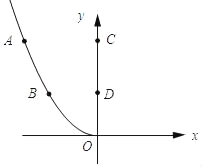
【题目】中国高铁迅猛发展，给我们的出行带来极大的便捷，如图1，是某种新设计动车车头的纵截面一部分，曲线OBA是一开口向左，对称轴正好是水平线OC的抛物线的一部分，点A、B是车头玻璃罩的最高点和最低点，AC、BD是两点到车厢底部的距离，OD=1.5米，BD=1.5米，AC=3米，请你利用所学的函数知识解决以下问题．

（1）为了方便研究问题，需要把曲线OBA绕点O旋转转化为我们熟悉的函数，请你在所给的方框内，画出你旋转后函数图象的草图，在图中标出点O、A、B、C、D对应的位置，并求你所画的函数的解析式．

（2）如图2，驾驶员座椅安装在水平线OC上一点P处，实验表明：当PA+PB最小时，驾驶员驾驶时视野最佳，为了达到最佳视野，求OP的长．

（3）驾驶员头顶到玻璃罩的高度至少为0.3米才感到压抑，一个驾驶员坐下时头顶到椅面的距离为1米，在（2）的情况下，座椅最多条件到多少时他才感到舒适？

Answer 1

【答案】（1）函数的解析式为y=x2（x≤0）；（2）OP= 3．（3）座椅最多调节得到0.8米时，他才感到舒适．

【解析】试题分析：（1）由图像的特点知，将曲线OBA绕点O逆时针旋转90°后变为我们熟悉的二次函数，旋转后点B的坐标为（﹣1.5，1.5），然后用待定系数法求出解析式；

（2）作点A关于OC的对称点A′，连结BA′交OC与点P．设DP=x，则PC=4.5﹣x，由

△CA′P∽△DBP列方程求解；

（3）将y=3代入（1）中所求的函数关系式，求出x的值，从而可求出答案.

解：（1）将曲线OBA绕点O逆时针旋转90°如图所示：则B（﹣1.5，1.5）．

设所画函数的解析式为y=ax2，将点B的坐标代入得： a=，解得：a=．

∴函数的解析式为y=x2．（x≤0）

（2）如下图所示：作点A关于OC的对称点A′，连结BA′交OC与点P．

由（1）可知OC=×32=6，则DC=OC﹣OD=4.5．

∵BD∥CA，

∴△CA′P∽△DBP．

∴=．

设DP=x，则PC=4.5﹣x．

∴=，解得：x=1.5．

∴DP=1.5．

∴OP=OD+DP=3．

（3）将y=3代入y=x2（x≤0），得： x2=3，解得：x=﹣或x=（舍去）．

∴点P到玻璃罩的高度=≈2.1．

∵2.1﹣0.3﹣1=0.8．

∴座椅最多调节得到0.8米时，他才感到舒适．