
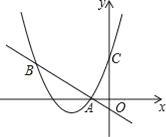
【题目】如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(﹣1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足(x+2)2+m≥kx+b的x的取值范围.
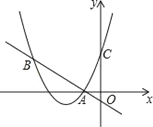
【答案】(1)抛物线解析式为y=x2+4x+3,一次函数解析式为y=﹣x﹣1;(2)由图象可知,满足(x+2)2+m≥kx+b的x的取值范围为x﹣4或x≥﹣1.
【解析】(1)先利用待定系数法先求出m,再求出点B坐标,利用方程组求出太阳还是解析式.
(2)根据二次函数的图象在一次函数的图象上面即可写出自变量x的取值范围.
解:(1)∵抛物线y=(x+2)2+m经过点A(﹣1,0),∴0=1+m,∴m=﹣1,∴抛物线解析式为y=(x+2)2﹣1=x2+4x+3,∴点C坐标(0,3),∵对称轴x=﹣2,B、C关于对称轴对称,∴点B坐标(﹣4,3),∵y=kx+b经过点A、B,
∴![]() ,解得
,解得![]() ,
,
∴一次函数解析式为y=﹣x﹣1,
(2)由图象可知,写出满足(x+2)2+m≥kx+b的x的取值范围为x<﹣4或x>﹣1.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.

(1)试说明:AB∥CD;
(2)若∠2=25°,求∠BFC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,若点P(4,3)在⊙O内,则⊙O的半径r的取值范围是( )
A. 0<r<4B. 3<r<4C. 4<r<5D. r>5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com