练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．先化简，再求值：（1+$\frac{1}{{a}^{2}-1}$）÷$\frac{a}{a+1}$，其中a是方程x2-2x=0的一个根．

    分析 原式括号中两项通分并利用同分母分式的加法法则计算，同时利用除法法则变形，约分得到最简结果，把a代入方程计算求出值即可．

    解答 解：原式=$\frac{{a}^{2}}{（a+1）（a-1）}$•$\frac{a+1}{a}$=$\frac{a}{a-1}$，
    把x=a代入方程得：a（a-2）=0，
    解得：a=0（舍去）或a=2，
    则原式=2．

    点评 此题考查了分式的化简求值，以及一元二次方程的解，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    5．甲、乙、丙三个仓库，各存放着数量相同的大米．用一台皮带输送机和12个工人，5小时可将甲仓库里的大米搬完；用一台皮带输送机和28个工人，3小时可将乙仓库内的大米搬完；现有2台皮带输送机，如果恰好用了2小时要将丙仓库内的大米搬完，还需要多少个工人同时搬运？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．某人的身份证号码是320802198003280535，则这个人的出生年月日是1980年3月28日．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

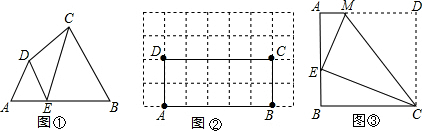    3．如图①，在四边形ABCD的边AB上任取一点E（点E不与A、B重合），分别连接ED、EC，可以把四边形ABCD分成三个三角形，如果其中有两个三角形相似，我们就把E叫做四边形ABCD的边AB上的“相似点”；如果这三个三角形都相似，我们就把E叫做四边形AB-CD的边AB上的“强相似点”，解决问题：
    （1）如图①，∠A=∠B=∠DEC=45°，试判断点E是否是四边形ABCD的边AB上的相似点，并说明理由：
    （2）如图②，在矩形ABCD中，A、B、C、D四点均在正方形网格（网格中每个小正方形的边长为1）的格点（即每个小正方形的顶点）上，试在图②中画出矩形ABCD的边AB上的强相似点；
    （3）如图③，将矩形ABCD沿CM折叠，使点D落在AB边上的点E处，若点E恰好是四边形ABCM的边AB上的
    一个强相似点，试证明$\frac{AB}{BC}$=$\frac{{2\sqrt{3}}}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．若正实数a、b满足ab=a+b+3，则a2+b2的最小值为（　　）
    A．-7B．2C．9D．18

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．下列各组中是全等形的是（　　）
    A．两个周长相等的等腰三角形B．两个面积相等的长方形
    C．两个面积相等的直角三角形D．两个周长相等的圆

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

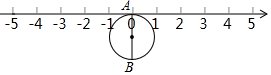    7．如图，半径为1个单位的圆片上有一点A与数轴上的原点重合，AB是圆片的直径．（注：结果保留π ）
    （1）把圆片沿数轴向右滚动半周，点B到达数轴上点C的位置，点C表示的数是无理数（填“无理”或“有理”），这个数是-π；
    （2）把圆片沿数轴滚动2周，点A到达数轴上点D的位置，点D表示的数是4π或-4π；
    （3）圆片在数轴上向右滚动的周数记为正数，圆片在数轴上向左滚动的周数记为负数，依次运动情况记录如下：+2，-1，+3，-4，-3．
    ①第4次滚动后，A点距离原点最近，第3次滚动后，A点距离原点最远．
    ②当圆片结束运动时，A点运动的路程共有26π，此时点A所表示的数是-6π．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

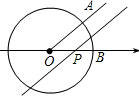    4．如图，已知⊙O是以数轴的原点O为圆心，半径为1的圆，∠AOB=45°，点P在数轴上运动，若过点P且与OA平行的直线与⊙O有公共点，设OP=x，则x的取值范围是0＜x≤$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．（1）如图①，求证：∠A+∠B=∠C+∠D．
    （2）如图②，求证：∠A+∠B+∠C=∠BDC．
    （3）如图③，则：∠A+∠B+∠C+∠D+∠E=180°．
    （4）如图④，则：∠A+∠B+∠C+∠D+∠E+∠F=360°．
    （5）如图⑤，则：∠A+∠B+∠C+∠D+∠E=180°．
    （6）如图⑥，则：∠A+∠B+∠C+∠D+∠E+∠F=360°．

    查看答案和解析>>

    同步练习册答案