
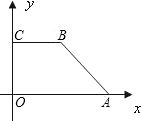
在直角梯形
OABC中,CB∥OA,Ð COA=90°,CB=3,OA=6,BA=3
(1)求点B的坐标;
(2)已知D、E分别为线段OC、OB上的点,OD=5,OE=2EB,直线DE交x轴于点F.求直线DE的解析式;
(3)点M是(2)中直线DE上的一个动点,在x轴上方的平面内是否存在另一个点N,使以O、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.
|
[解](1)如图,作BH^ x轴于点H,则四边形OHBC为矩形, ∴OH=CB=3,∴AH=OA-OH=6-3=3, 在 Rt△ABH中,BH=∴点B的坐标为(3,6).
(2)如上图,作EG^ x轴于点G,则EG∥BH, ∴△OEG~△OBH,∴ ∴ 又 ∵点D的坐标为(0,5),设直线DE的解析式为y=kx+b,则(3)答:存在. ①如图,当 OD=DM=MN=NO=5时,四边形ODMN为菱形.作MP^ y轴于点P,则 MP∥x轴,∴△MPD~△FOD,∴又 ∵当y=0时,-在 Rt△ODF中,FD=∴MP=2 ∴点N的坐标为(-2 ②如图,当 OD=DN=NM=MO=5时,四边形ODNM为菱形.延长NM交x轴于点P,则MP^ x轴.∵点M在直线y=-
∴点M的坐标为(4,3),∴点N的坐标为(4,8). ③如图,当 OM=MD=DN=NO时,四边形OMDN为菱形.连接NM,交OD于点P,则NM与OD互相垂直平分,∴yM=yN=OP=∴xN=-xM=-5,∴点N的坐标为(-5, 综上所述, x轴上方的点N有三个,分别为N1(-2N2(4,8),N3(-5,
|


科目:初中数学 来源: 题型:
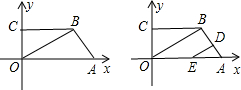
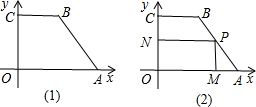 如图(1),在直角梯形OABC中,BC∥OA,∠OCB=90°,OA=6,AB=5,cos∠OAB=
如图(1),在直角梯形OABC中,BC∥OA,∠OCB=90°,OA=6,AB=5,cos∠OAB=| 3 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•高淳县二模)如图,在直角梯形OABC中,OA∥BC,A、B两点的坐标分别为A(13,0),B(11,12).动点P、Q分别从O、B两点同时出发,点P以每秒3个单位的速度沿射线OA运动,点Q以每秒1个单位的速度沿线段BC运动,当点Q运动到C点时,P、Q同时停止运动,动点P、Q运动时间为t秒.设线段PQ和OB相交于点D,过点D作DE∥OA交AB于点E,射线QE交x轴于点F.
(2013•高淳县二模)如图,在直角梯形OABC中,OA∥BC,A、B两点的坐标分别为A(13,0),B(11,12).动点P、Q分别从O、B两点同时出发,点P以每秒3个单位的速度沿射线OA运动,点Q以每秒1个单位的速度沿线段BC运动,当点Q运动到C点时,P、Q同时停止运动,动点P、Q运动时间为t秒.设线段PQ和OB相交于点D,过点D作DE∥OA交AB于点E,射线QE交x轴于点F.查看答案和解析>>
科目:初中数学 来源: 题型:
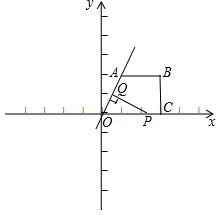 如图,在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,2),C(3,0).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ⊥直线OA,垂足为Q.设P点移动的时间为t秒(0<t≤7),△OPQ与直角梯形OABC重叠部分的面积为S.
如图,在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,2),C(3,0).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ⊥直线OA,垂足为Q.设P点移动的时间为t秒(0<t≤7),△OPQ与直角梯形OABC重叠部分的面积为S.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com