
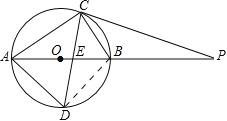
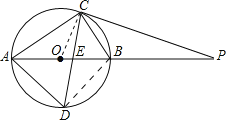
【题目】如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.

(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由.
【答案】(1)AC=8,AD=5![]() cm;(2)直线PC与⊙O相切,理由见解析.
cm;(2)直线PC与⊙O相切,理由见解析.
【解析】试题分析:(1)、连接BD,根据AB为直径,则∠ACB=∠ADB=90°,根据Rt△ABC的勾股定理求出AC的长度,根据CD平分∠ACB得出Rt△ABD是等腰直角三角形,从而得出AD的长度;(2)、连接OC,根据OA=OC得出∠CAO=∠OCA,根据PC=PE得出∠PCE=∠PEC,然后结合CD平分∠ACB得出∠ACE=∠ECB,从而得出∠PCB=∠ACO,根据∠ACB=90°得出∠OCP=90°,从而说明切线.
试题解析:(1)、①如图,连接BD, ∵AB是直径, ∴∠ACB=∠ADB=90°,
在RT△ABC中,AC=![]() =
=![]() =8cm,
=8cm,
②∵CD平分∠ACB, ∴AD=BD,∴Rt△ABD是直角等腰三角形, ∴AD=![]() AB=
AB=![]() ×10=5
×10=5![]() cm;
cm;
(2)、直线PC与⊙O相切,
理由:连接OC, ∵OC=OA,∴∠CAO=∠OCA, ∵PC=PE, ∴∠PCE=∠PEC,
∵∠PEC=∠CAE+∠ACE, ∵CD平分∠ACB, ∴∠ACE=∠ECB,∴∠PCB=∠ACO,∵∠ACB=90°,
∴∠OCP=∠OCB+∠PCB=∠ACO+∠OCB=∠ACB=90°, OC⊥PC,
∴直线PC与⊙O相切.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】阅读:因为一个非负数的绝对值等于它本身,负数的绝对值等于它的相反数,所以当a≥0时|a|=a,当a<0时|a|=﹣a,根据以上阅读完成:
(1)|3.14﹣π|= .
(2)计算:| ![]() ﹣1|+|
﹣1|+| ![]() ﹣
﹣ ![]() |+|
|+| ![]() ﹣
﹣ ![]() |…+|
|…+| ![]() ﹣
﹣ ![]() |+|
|+| ![]() +
+ ![]() |.
|.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条河的水流速度是1.8km/h,某条船在静水中的速度是akm/h,则该船在这条河中逆流行驶的速度是( )
A. (a+1.8)km/h B. (a﹣1.8)km/h
C. (a+3.6)km/h D. (a﹣3.6)km/h
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种商品每件成本a元,原来按成本增加22%定出价格,由于库存积压减价,按照原价的85%出售,则现售价是( )
A. 85%(a+22%)元 B. 15%(1+22%)a元
C. (a+22%+85%)元 D. 85%(1+22%)a元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD. 
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=100°,∠D=30°,求∠AEM的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据调查,超速行驶是引发交通事故的主要原因之一.上周末,小明和三位同学用所学过的知识在一条笔直的道路上检测车速.如图,观测点C到公路的距离CD为100米,检测路段的起点A位于点C的南偏西60°方向上,终点B位于点C的南偏西45°方向上.某时段,一辆轿车由西向东匀速行驶,测得此车由A处行驶到B处的时间为4秒. 问此车是否超过了该路段16米/秒的限制速度?(参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com