
计算:(1)![]() ·
·![]() +cot(
+cot(![]() -α)·cotα=________(α为锐角);
-α)·cotα=________(α为锐角);
(2)![]() -|2
-|2![]() -
-![]() |-
|-![]() -
-![]() =________;
=________;
(3)![]() (2
(2![]() -
-![]() )+(4-5π)0-(
)+(4-5π)0-(![]() -1)-1=________.
-1)-1=________.
科目:初中数学 来源: 题型:
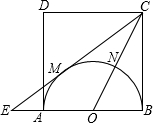 半圆O于点N.
半圆O于点N.查看答案和解析>>
科目:初中数学 来源: 题型:
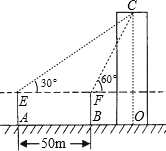 如图,小平为了测量学校教学楼的高度,她先在A处利用测角仪测得楼顶C的仰角为30°,再向楼的方向直行50米到达B处,又测得楼顶C的仰角为60度.已知测角仪的高度是1.2米,请你帮助小平计算出学校教学楼的高度CO.(
如图,小平为了测量学校教学楼的高度,她先在A处利用测角仪测得楼顶C的仰角为30°,再向楼的方向直行50米到达B处,又测得楼顶C的仰角为60度.已知测角仪的高度是1.2米,请你帮助小平计算出学校教学楼的高度CO.(| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
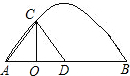 的坐标(坐标轴上的一个长度单位为1m);
的坐标(坐标轴上的一个长度单位为1m);查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com