
 如图,已知AB=AC,DE垂直平分AB,若∠A=40°,则∠EBC=30°.
如图,已知AB=AC,DE垂直平分AB,若∠A=40°,则∠EBC=30°.  一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
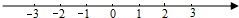 解不等式组$\left\{\begin{array}{l}2x-1≤x+2,①\\ \frac{3x+1}{5}+2≥1.②\end{array}\right.$请结合题意填空,完成本题的解答.
解不等式组$\left\{\begin{array}{l}2x-1≤x+2,①\\ \frac{3x+1}{5}+2≥1.②\end{array}\right.$请结合题意填空,完成本题的解答.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知锐角△ABC中,边BC长为90,高AD长为60,矩形EFGH的边GH在BC边上,其余两个顶点E,F分别在AB,AC上,EF交AD于点K.
如图,已知锐角△ABC中,边BC长为90,高AD长为60,矩形EFGH的边GH在BC边上,其余两个顶点E,F分别在AB,AC上,EF交AD于点K.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 2015年以来.安徽省高速公路建设稳步推进,相继有十条高速公路建成通车.实现了所有的县在半小时内通达高速.全省高速公路通车里程突破4200公里.如图是某高速单向过山隧道截面设计图.隧道横截面呈抛物线形,设计AB=6米,最高点P点距地面8米.
2015年以来.安徽省高速公路建设稳步推进,相继有十条高速公路建成通车.实现了所有的县在半小时内通达高速.全省高速公路通车里程突破4200公里.如图是某高速单向过山隧道截面设计图.隧道横截面呈抛物线形,设计AB=6米,最高点P点距地面8米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com