练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    完成下面证明

    已知：如图,∠COF＋∠C=，∠C=∠B．

    求证：AB∥EF．

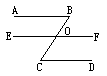
    证明：∵∠COF＋∠C=(已知)，

    ∴________(　　)

    又∵∠C=∠B(已知)，

    ∴________(　　)

    ∴AB∥EF(　　)

    　

    答案：(1)EF∥CD,同旁内角互补,两直线平行,AB∥CD,内错角相等,两直线平行（2）垂直定义，互余定义，同角的余角相等
    解析：

    (1)EF∥CD,同旁内角互补,两直线平行,AB∥CD,内错角相等,两直线平行,平行于同一直线的两直线平行

    (2)垂直定义，互余定义，同角的余角相等


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

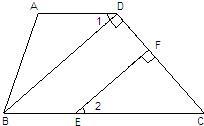    19、如图，在四边形ABCD中，∠A=104°-∠2，∠ABC=76°+∠2，BD⊥CD于D，EF⊥CD于F．
    求证：∠1=∠2．请你完成下面证明过程．
    证明：因为∠A=104°-∠2，∠ABC=76°+∠2，（
    已知
    ）
    所以∠A+∠ABC=104°-∠2+76°+∠2，（等式性质）
    即∠A+∠ABC=180°
    所以AD∥BC，（
    同旁内角互补，两直线平行
    ）
    所以∠1=∠DBC，（
    两直线平行，内错角相等
    ）
    因为BD⊥DC，EF⊥DC，（
    已知
    ）
    所以∠BDC=90°，∠EFC=90°，（
    垂线的定义
    ）
    所以∠BDC=∠EFC，
    所以BD∥
    EF
    ，（
    同位角相等，两直线平行
    ）
    所以∠2=∠DBC，（
    两直线平行，同位角相等
    ）
    所以∠1=∠2（
    等量代换
    ）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

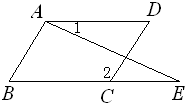    25、学着说点理：完成下面证明，并注明理由
    已知：如图，∠1=∠E，∠B=∠D．
    求证：AB∥CD．
    证明：因为∠1=∠E（
    已知．
    ）
    所以 
    AD．
    ∥
    BC．
       （
    内错角相等，两直线平行．
    ）
    所以∠D+∠2=180° （
    两直线平行，同旁内角互补．
    ）
    因为∠B=∠D
    所以∠
    B．
    +∠
    2．
    =180°
    所以 AB∥CD（
    同旁内角互补，两直线平行．
    ）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    完成下面证明：

    （1）如图1，已知直线b∥c，a⊥c，求证：a⊥b
    证明：∵a⊥c  （已知）
    ∴∠1=
    ∠2
    ∠2
    （垂直定义）
    ∵b∥c （已知）
    ∴∠1=∠2  （
    两直线平行，同位角相等
    两直线平行，同位角相等
    ）
    ∴∠2=∠1=90° （
    等量代换
    等量代换
    ）
    ∴a⊥b      （
    垂直的定义
    垂直的定义
    ）
    （2）如图2：AB∥CD，∠B+∠D=180°，求证：CB∥DE
    证明：∵AB∥CD （已知）
    ∴∠B=
    ∠C
    ∠C
    （
    两直线平行，内错角相等
    两直线平行，内错角相等
    ）
    ∵∠B+∠D=180° （已知）
    ∴∠C+∠D=180° （
    等量代换
    等量代换
    ）
    ∴CB∥DE   （
    同旁内角互补，两直线平行
    同旁内角互补，两直线平行
    ）

    查看答案和解析>>

    科目：初中数学 来源：2000～2001学年度第二学期初一数学形成性教学评估 平行线、命题、定理、证明 题型：022

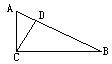
    完成下面证明

    已知：如图，AC⊥BC，垂足为C，∠BCD是∠B的余角，

    求证：∠ACD=∠B．

    证明：∵AC⊥BC(已知)，

    ∴∠ACB=(　　)

    ∴∠BCD是∠ACD的余角(　　)

    ∵∠BCD是∠B的余角(已知)，

    ∴∠ACB=∠B．(　　)

    查看答案和解析>>

    同步练习册答案