
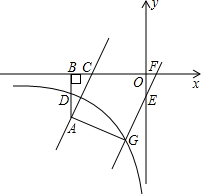
 如图,点A在反比例函数y=
如图,点A在反比例函数y=| k |
| x |
| k |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 12 |
| x |
|
|
|
|
|
 ∴G(-2,-6),
∴G(-2,-6),| 22+42 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图,一次函数y=kx-1的图象与坐标轴分别交于A、B两点,与反比例函数y=
如图,一次函数y=kx-1的图象与坐标轴分别交于A、B两点,与反比例函数y=| m |
| x |
| m |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
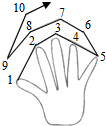 请同学们伸出左手,一起做下面的游戏:从大拇指开始,依次数数字1、2、3、4、5,然后从无名指开始倒着数6、7、8、9,再从食指开始数10、11、12、13,…请问数字20落在哪个手指上?200?2000呢?
请同学们伸出左手,一起做下面的游戏:从大拇指开始,依次数数字1、2、3、4、5,然后从无名指开始倒着数6、7、8、9,再从食指开始数10、11、12、13,…请问数字20落在哪个手指上?200?2000呢?查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,梯形ABCD中,AD∥BC,∠BAD=90°,AD=7cm,BC=4cm,AB=4cm,现有动点P以3cm/s的速度从点A向点D运动,动点Q以2cm/s的速度从点C向点B运动,若P,Q两点同时出发,一个点停止运动时另一个点也停止运动,连接AQ、PQ,设运动时间为x s,请问x为何值时,△APQ为等腰三角形.
如图,梯形ABCD中,AD∥BC,∠BAD=90°,AD=7cm,BC=4cm,AB=4cm,现有动点P以3cm/s的速度从点A向点D运动,动点Q以2cm/s的速度从点C向点B运动,若P,Q两点同时出发,一个点停止运动时另一个点也停止运动,连接AQ、PQ,设运动时间为x s,请问x为何值时,△APQ为等腰三角形.查看答案和解析>>
科目:初中数学 来源: 题型:
 (1)已知⊙O的直径为10cm,点A为⊙O外一定点,OA=12cm,点P为⊙O上一动点,求PA的最大值和最小值.
(1)已知⊙O的直径为10cm,点A为⊙O外一定点,OA=12cm,点P为⊙O上一动点,求PA的最大值和最小值. |
| AC |
 |
| CB |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
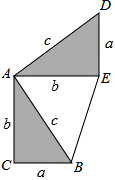 勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中常见的是“面积法”,当两个全等的直角三角形如图摆放时(其中∠DAB=90°),就可以用“面积法”来证明勾股定理,即证明a2+b2=c2,请你写出勾股定理的证明过程.
勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中常见的是“面积法”,当两个全等的直角三角形如图摆放时(其中∠DAB=90°),就可以用“面积法”来证明勾股定理,即证明a2+b2=c2,请你写出勾股定理的证明过程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com