
【题目】如图,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1.0,1.21,1.44,正放置的四个正方形的面积为S1、S2、S3、S4,则S1+S2+S3+S4= .
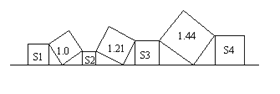
【答案】2.44
【解析】
由条件可以得出AC=CF=1,FH=LH=1.1,PR=SR=1.2.由正方形的性质可以得出∠ACB=∠CED,∠FHG=∠HLM,∠PRN=∠RST,就可以得出△ABC≌△CDE,△FGH≌△HML,△PNR≌△RTS,就可以得出AB=CD,BC=DE,FG=HM,GH=ML,PN=RT,NR=ST,由勾股定理就可以AB2+BC2=AC2,FG2+GH2=FH2,NP2+NR2=PR2,由正方形的面积公式就可以得出结论.
解:如图,

∵斜放置的三个正方形的面积分别为1,1.21,1.44,
∴AC=CF=1,FH=LH=1.1,PR=SR=1.2.∠ACD=∠FHL=∠PRS=90°,
∴∠ACB=∠CED,∠FHG=∠HLM,∠PRN=∠RST,
∴△ABC≌△CDE,△FGH≌△HML,△PNR≌△RTS,
∴AB=CD,BC=DE,FG=HM,GH=ML,PN=RT,NR=ST,
由勾股定理,得
AB2+BC2=AC2,FG2+GH2=FH2,NP2+NR2=PR2,
∴S1+S2=1.0,S2+S3=1.21,S3+S4=1.44,
∴S1+S2+S2+S3+S3+S4=1+1.21+1.44=3.65,
∴S1+2S2+2S3+S4=3.65.
∴S1+S2+S3+S4=2.44.
故答案为:2.44.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.

(1)概念理解:
如图1,在△ABC中,AC=6,BC=3,∠ACB=30°,试判断△ABC是否是”等高底”三角形,请说明理由.
(2)问题探究:
如图2,△ABC是“等高底”三角形,BC是”等底”,作△ABC关于BC所在直线的对称图形得到△A'BC,连结AA′交直线BC于点D.若点B是△AA′C的重心,求![]() 的值.
的值.
(3)应用拓展:
如图3,已知l1∥l2,l1与l2之间的距离为2.“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的![]() 倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B和∠C的平分线交于点I,边AB和AC的垂直平分线交于点O,若∠BIC=90°+![]() θ,则∠BOC=( )
θ,则∠BOC=( )
A.90°﹣![]() θB.2θC.180°﹣θD.以上答案都不对
θB.2θC.180°﹣θD.以上答案都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节是我国的传统节日,人们素有吃粽子的习俗,某商场在端午节来临之际用3000元购进![]() 、
、![]() 两种粽子1100个,购买
两种粽子1100个,购买![]() 种粽子与购买
种粽子与购买![]() 种粽子的费用相同,已知
种粽子的费用相同,已知![]() 粽子的单价是
粽子的单价是![]() 种粽子单价的1.2倍.
种粽子单价的1.2倍.
(1)求![]() 、
、![]() 两种粽子的单价各是多少?
两种粽子的单价各是多少?
(2)若计划用不超过7000元的资金再次购买![]() 、
、![]() 两种粽子共2600个,已知
两种粽子共2600个,已知![]() 、
、![]() 两种粽子的进价不变,求
两种粽子的进价不变,求![]() 中粽子最多能购进多少个?
中粽子最多能购进多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】台州某校七(1)班同学分三组进行数学活动,对七年级400名同学最喜欢喝的饮料情况、八年级300名同学零花钱的最主要用途情况、九年级300名同学完成家庭作业时间情况进行了全面调查,并分别用扇形图、频数分布直方图、表格来描述整理得到的数据.
根据以上信息,请回答下列问题:
(1)七年级400名同学中最喜欢喝“冰红茶”的人数是多少?
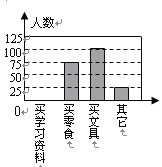
(2)补全八年级300名同学中零花钱的最主要用途情况频数分布直方图;
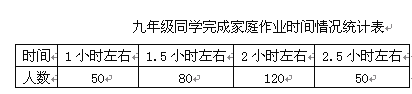
(3)九年级300名同学中完成家庭作业的平均时间大约是多少小时(结果保留一位小数)?

![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四个命题中,真命题的个数有( )
①数轴上的点和有理数是一一对应的;
②![]() 中,已知两边长分别是3和4,则第三条边长为5;
中,已知两边长分别是3和4,则第三条边长为5;
③在平面直角坐标系中点(2,-3)关于y轴对称的点的坐标是(-2,-3);
④两条直线被第三条直线所截,内错角相等.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
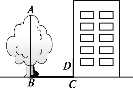
【题目】小琳同学学习了《太阳光与影子》这一节以后,就想利用树影测量树高,但这棵树离大楼太近,影子不全落在地上,有一部分影子落在墙上(如图),她在某时刻测得留在墙上的影长为1.2 m,测得地面上的影长为2.7 m,巧的是她拿的竹竿的长也是1.2 m,竹竿的影长为1.08 m,她是怎样求得树高AB的?结果是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药厂销售部门根据市场调研结果,对该厂生产的一种新型原料药未来两年的销售进行预测,井建立如下模型:设第t个月该原料药的月销售量为P(单位:吨),P与t之间存在如图所示的函数关系,其图象是函数P=![]() (0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=
(0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=![]()
(1)当8<t≤24时,求P关于t的函数解析式;
(2)设第t个月销售该原料药的月毛利润为w(单位:万元)
①求w关于t的函数解析式;
②该药厂销售部门分析认为,336≤w≤513是最有利于该原料药可持续生产和销售的月毛利润范围,求此范围所对应的月销售量P的最小值和最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com