
����Ŀ��ij�̳������ס������ֿյ���50̨����֪����һ̨���ֿյ��ȹ���һ̨���ֿյ�������0.3��Ԫ����20��Ԫ�������ֿյ���������40��Ԫ�������ֿյ�������2���������������⣺
��1����ס������ֿյ�ÿ̨���۸��Ƕ�����Ԫ��
��2�����̳�Ԥ��Ͷ���ʽ�����10��Ԫ���ҹ������ֿյ�����31̨���̳����ļ��ֹ���������
��3���ڣ�2�������£������ֿյ�ÿ̨�ۼ�1100Ԫ�����ֿյ�ÿ̨�ۼ�4300Ԫ���ס��ҿյ�����һ̨���������۳��ۣ�����ȫ������۳����̳���������50̨�յ��������ó�2520Ԫ��ΪԱ����������������ǡ���ֿ��Թ������Ͽյ���2̨����ֱ��д�����̳�������50̨�յ�����̨��
���𰸡���1��0.1��0.4����2���̳���3�ֹ����������ٹ�����ֿյ�31̨���������ֿյ�19̨���ڹ�����ֿյ�32̨���������ֿյ�18̨���۹�����ֿյ�33̨���������ֿյ�17̨����3��������ֿյ�32̨���������ֿյ�18̨
��������
��1��������ֿյ�ÿ̨������x��Ԫ�������ֿյ�ÿ̨�����ǣ�x+0.3����Ԫ�����ݵ�����ϵ��20��Ԫ�������ֿյ���������40��Ԫ�������ֿյ�������2���г�������⼴�ɣ�
��2���蹺����ֿյ�n̨���������ֿյ���50��n��̨�������̳�Ԥ��Ͷ���ʽ�����10��Ԫ���ҹ������ֿյ�����31̨�����n�ķ�Χ������ȷ����������
��3���ҵ���2����3�ֹ����������������ļ�Ϊ����
�⣺��1������ֿյ�ÿ̨������x��Ԫ�������ֿյ�ÿ̨�����ǣ�x+0.3����Ԫ����������
![]() ��
��![]() ��2��
��2��
���x��0.1��
x+0.3��0.1+0.3��0.4��
�𣺼��ֿյ�ÿ̨������0.1��Ԫ�����ֿյ�ÿ̨������0.4��Ԫ��
��2���蹺����ֿյ�n̨���������ֿյ���50��n��̨����������
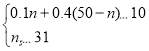 ��
��
���31��n��33![]() ��
��
��n������
��nȡ31��32��33��
���̳���3�ֹ����������ٹ�����ֿյ�31̨���������ֿյ�19̨���ڹ�����ֿյ�32̨���������ֿյ�18̨���۹�����ֿյ�33̨���������ֿյ�17̨��
��3���ٹ�����ֿյ�31̨���������ֿյ�19̨��
��31��1������1100��1000��+��1100��0.8��1000��+��19��1������4300��4000��+��4300��0.8��4000����2520
��3000��120+5400��560��2520
��7720��2520
��5200��Ԫ����
���������⣬��ȥ��
�ڹ�����ֿյ�32̨���������ֿյ�18̨��
��32��1������1100��1000��+��1100��0.8��1000��+��18��1������4300��4000��+��4300��0.8��4000����2520
��3100��120+5100��560��2520
��7520��2520
��5000��Ԫ����
�������⣻
�۹�����ֿյ�33̨���������ֿյ�17̨��
��33��1������1100��1000��+��1100��0.8��1000��+��17��1������4300��4000��+��4300��0.8��4000����2520
��3200��120+4800��560��2520
��7320��2520
��4800��Ԫ����
���������⣬��ȥ��
����������������ֿյ�32̨���������ֿյ�18̨��


 ����Ӣ��ϵ�д�
����Ӣ��ϵ�д� ����ѧУ�ֲ����ܲ�ϵ�д�
����ѧУ�ֲ����ܲ�ϵ�д� �ƸԺ���ȫ�����Ų��Ծ�ϵ�д�
�ƸԺ���ȫ�����Ų��Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У���һ������
�У���һ������![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ���ֽ�������ȫ��ͬ������ֱ������
���ֽ�������ȫ��ͬ������ֱ������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ſ�Ƭϴ�Ⱥ��泯�ϣ�������ȡһ�ţ����ÿ�Ƭ�ϵ�����Ϊ��
�ſ�Ƭϴ�Ⱥ��泯�ϣ�������ȡһ�ţ����ÿ�Ƭ�ϵ�����Ϊ��![]() �ĺ����꣬��������ƽ����Ϊ��
�ĺ����꣬��������ƽ����Ϊ��![]() �������꣬���
�������꣬���![]() ������������
������������![]() ��Χ�ɵ������ڣ����߽磩�ĸ���Ϊ________��
��Χ�ɵ������ڣ����߽磩�ĸ���Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �߳�Ϊ
�߳�Ϊ![]() �ĵȱ�������
�ĵȱ�������![]() �Ķ���
�Ķ���![]() �ֱ��ڱ�
�ֱ��ڱ�![]() ��
��![]() �ϵ�
�ϵ�![]() �ڱ�
�ڱ�![]() ���˶�ʱ��
���˶�ʱ��![]() ��֮�ڱ�
��֮�ڱ�![]() ���˶����ȱ������ε���״���ֲ��䣬�˶������У���
���˶����ȱ������ε���״���ֲ��䣬�˶������У���![]() ����
����![]() ���������� ��
���������� ��

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ��OΪ����ԭ�㣬��A����2��0������B��0��2![]() ����
����

��1��ֱ��д���BAO�Ķ�����
��2����ͼ1������AOB�Ƶ�O˳ʱ�����A��OB������A��ǡ������AB����ʱ������AB��O�����ΪS1����BA��O�����ΪS2��S1��S2�кι�ϵ��Ϊʲô��
��3��������AOB�Ƶ�O˳ʱ����ת����ͼ2��ʾ��λ�ã�S1��S2�Ĺ�ϵ�����仯����֤������жϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A��1��2����B��3��1����C����2����1����
��1����ͼ��������ABC����y��ԳƵ���A1B1C1��д����A1��B1��C1�����ֱ꣨��д�𰸣���
��2����A1B1C1������� ����
��3����y���ϻ�����Q��ʹ��QAB���ܳ���С��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������п������ؿ���Ŀ֮һ��������ijѧУΪ�˽������꼶ѧ�������������������������ȡ���־��꼶ѧ����������IJ��Գɼ���Ϊһ����������A��B��C��D�ĸ��ȼ�����ͳ�ƣ��Ƴ������²�������ͳ��ͼ����˵����A����8�֩�10�֣�B����7�֩�7.9�֣�C����6�֩�6.9�֣�D����1�֩�5.9�֣�
����������Ϣ������������⣺
��1��������ͳ��ͼ�У�C��Ӧ�����ε�Բ�Ľ���_____�ȣ�
��2����ȫ����ͳ��ͼ��
��3������ȡѧ��������������Գɼ�����λ��������_____�ȼ���
��4����У���꼶��300��ѧ�������������������Գɼ��ﵽA����ѧ���ж����ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB��AC��ADΪ��BC�ϵ����ߣ���E��AD�ϣ��Ե�AΪԲ�ģ�AB��Ϊ�뾶��������BE���ӳ����ڵ�F����G��EF�ϣ��ҡ�EAG����CAF������CE��
��1�������ⲹȫͼ�Σ�
��2����֤��FG��CE��
��3����EFƽ�֡�AEC�����BAE���ABE����ĵ�����ϵΪ�� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����EΪ����ABCD�ı�AD��һ�㣬��P�ӵ�B������BE��ED��DC�˶�����Cֹͣ����Q�ӵ�B������BC�˶�����Cֹͣ�������˶����ٶȶ���1cm/s������P��Qͬʱ��ʼ�˶������˶�ʱ��Ϊt��s������BPQ�����Ϊy��cm2������֪y��t֮��ĺ���ͼ����ͼ2��ʾ���������н��ۣ�����0��t��10ʱ����BPQ�ǵ��������Σ���S��ABE=48cm2����14��t��22ʱ��y=110��5t�������˶������У�ʹ����ABP�ǵ��������ε�P��һ����3����������BPQ����BEA����ʱ��t=14.5��������ȷ���۵�����ǣ�������

A. �٢ܢ� B. �٢ڢ� C. �٢ۢ� D. �٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() �ֱ�
�ֱ�![]() �ᡢ
�ᡢ![]() ���ڵ�
���ڵ�![]() �͵�
�͵�![]() ����
����![]() ��
��![]() ����
����![]() .
.

��1��![]() ______��
______��![]() ______.
______.
��2����![]() ��ֱ��
��ֱ��![]() ���Ҳ࣬��
���Ҳ࣬��![]() ��
��
������![]() ��
��![]() ���ϣ����
���ϣ����![]() ������Ϊ______��
������Ϊ______��
����![]() Ϊֱ�������Σ����
Ϊֱ�������Σ����![]() ������.
������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com