
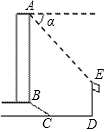
 如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杆顶端E的俯角α是45°,旗杆低端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:$\sqrt{3}$,则大楼AB的高度为6$\sqrt{3}$+29米.
如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杆顶端E的俯角α是45°,旗杆低端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:$\sqrt{3}$,则大楼AB的高度为6$\sqrt{3}$+29米. 分析 延长AB交DC于H,作EG⊥AB于G,则GH=DE=15米,EG=DH,设BH=x米,则CH=$\sqrt{3}$x米,在Rt△BCH中,BC=12米,由勾股定理得出方程,解方程求出BH=6米,CH=6$\sqrt{3}$米,得出BG、EG的长度,证明△AEG是等腰直角三角形,得出AG=EG=6$\sqrt{3}$+20(米),即可得出大楼AB的高度.
解答 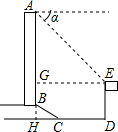 解:延长AB交DC于H,作EG⊥AB于G,如图所示:
解:延长AB交DC于H,作EG⊥AB于G,如图所示:
则GH=DE=15米,EG=DH,
∵梯坎坡度i=1:$\sqrt{3}$,
∴BH:CH=1:$\sqrt{3}$,
设BH=x米,则CH=$\sqrt{3}$x米,
在Rt△BCH中,BC=12米,
由勾股定理得:x2+($\sqrt{3}$x)2=122,
解得:x=6,∴BH=6米,CH=6$\sqrt{3}$米,
∴BG=GH-BH=15-6=9(米),EG=DH=CH+CD=6$\sqrt{3}$+20(米),
∵∠α=45°,
∴∠EAG=90°-45°=45°,
∴△AEG是等腰直角三角形,
∴AG=EG=6$\sqrt{3}$+20(米),
∴AB=AG+BG=6$\sqrt{3}$+20+9=(6$\sqrt{3}$+29)m.
故答案为:6$\sqrt{3}$+29.
点评 本题考查了解直角三角形的应用-坡度、俯角问题;通过作辅助线运用勾股定理求出BH,得出EG是解决问题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
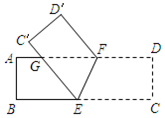 如图,将一张长方形纸片ABCD沿EF折叠,使顶点C,D分别落在点C′,D′处,C′E交AF于点G,若∠CEF=80°,则∠GFD′=20°.
如图,将一张长方形纸片ABCD沿EF折叠,使顶点C,D分别落在点C′,D′处,C′E交AF于点G,若∠CEF=80°,则∠GFD′=20°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com