
【题目】如下表,从左到右在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,则第![]() 个格子的数为_____.
个格子的数为_____.
![]()
科目:初中数学 来源: 题型:
【题目】小明去文具用品商店给同学买某品牌水性笔,已知甲、乙两商店都有该品牌的水性笔,标价都是2元/支,但甲、乙两商店的优惠条件却不同.
甲商店:若购买不超过10支,则按标价付款;若一次购10支以上,则超过10支的部分按标价的60%付款.
乙商店:按标价的80%付款
在水性笔的质量等因素相同的条件下:
(1)设小明要购买的该品牌笔数是x(x>10)支,则甲商店购买水性笔的费用为 元;乙商店购买水性笔的费用为 元;(用含x的代数式表示,并化简.)
(2)若小明要购买该品牌笔30支,你认为在甲、乙两商店中,到哪个商店购买比较省钱?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
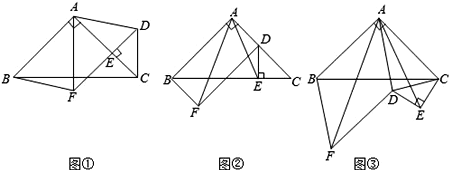
【题目】如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系 ;
(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年1月的日历表如表所示:
日 | 一 | 二 | 三 | 四 | 五 | 六 |
1 | 2 | 3 | 4 | |||
5 | 6 | 7 | 8 | 9 | 10 | 11 |
12 | 13 | 14 | 15 | 16 | 17 | 18 |
19 | 20 | 21 | 22 | 23 | 24 | 25 |
26 | 27 | 28 | 29 | 30 | 31 |
快到放寒假了,班主任孙老师看日历届时准备安排一节假期安全班会课,孙老师把日历与本学期书本上73页的数学活动3联系在一起,经过思索后,孙老师给孩子们展示两个问题:
(1)若连续三天的号数之和等于48,那么这三天分别是几号?
(2)用一个“T”字形的框在表中框出四个数,这四个数的和能等于83吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
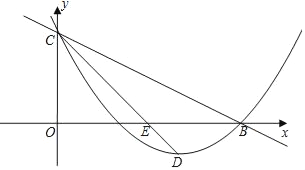
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2﹣2x+c与直线y=﹣![]() x+3分别交于x轴、y轴上的B、C两点,抛物线的顶点为点D,联结CD交x轴于点E.
x+3分别交于x轴、y轴上的B、C两点,抛物线的顶点为点D,联结CD交x轴于点E.
(1)求抛物线的解析式以及点D的坐标;
(2)求tan∠BCD;
(3)点P在直线BC上,若∠PEB=∠BCD,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列各题并按要求完成:
(1)定义:若两个一元二次方程有一个相同的实数根,则称这两个方程为“友好方程”,已知关于x的一元二次方程 x 2x 0 与 x 3x m 1 0 为“友好方程”,求 m 的值;
(2)关于x的一元二次方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() ,
,![]() ,且二次根式
,且二次根式![]() 有意义,若T=
有意义,若T=![]() ,求T的取值范围;
,求T的取值范围;
(3)我们不妨约定方程的整数解称之为“硬核”,例如x=1就称为方程(x-1)(2x+1)=0 的一个“硬核”,若一元二次方程(k-3k+2)x+(2k-4k+1)x+k-k=0(k为常数)有两个不同的“硬核”,试确定方程的两个“硬核”及常数 k 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.
(1)求∠AOE的度数;
(2)若OF平分∠BOE,问:OB是∠DOF的平分线吗?试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:我国数学家华罗庚在一次出国访问途中,看到飞机上:邻座的乘客阅读的杂志上有一道智力题,求59319的立方根,华罗庚脱口而击.众人惊命,忙问计算奥妙.你知道怎样迅速准确地计算出结果的吗?诺按照下面的分析试一试
(1)由103=1000,1003=100000,可知![]() 是 位数;
是 位数;
(2)由59319的个位数是9,可知![]() 的个位数是 ;
的个位数是 ;
(3)如果划去59319后面的三位319得到59,而33=27,43=64,由此确定![]() 的十位数是 .
的十位数是 .
请应用以上方法计算:![]() = .
= . ![]() =
=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①△ABF≌△CBF;②点E到AB的距离是2![]() ;③tan∠DCF=
;③tan∠DCF=![]() ;④△ABF的面积为
;④△ABF的面积为![]() .其中一定成立的有几个( )
.其中一定成立的有几个( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com