
 如图所示,△ABC是等腰直角三角形,∠ACB=90°,直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让△ABC沿这条直线向右平移,直到点A与点E重合为止.设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )
如图所示,△ABC是等腰直角三角形,∠ACB=90°,直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让△ABC沿这条直线向右平移,直到点A与点E重合为止.设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )| A. |  | B. | 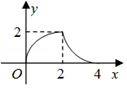 | C. | 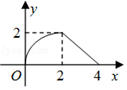 | D. | 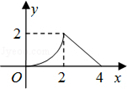 |
分析 此题可分为两段求解,即C从D点运动到E点和A从D点运动到E点,列出面积随动点变化的函数关系式即可.
解答 解:设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y∴
当C从D点运动到E点时,即0≤x≤2时,y=$\frac{1}{2}$×2×2-$\frac{1}{2}$(2-x)×(2-x)=-$\frac{1}{2}$x2+2x.
当A从D点运动到E点时,即2<x≤4时,y=$\frac{1}{2}$×[2-(x-2)]×[2-(x-2)]=$\frac{1}{2}$x2-4x+8,
∴y与x之间的函数关系 $\left\{\begin{array}{l}{y=-\\ \frac{1}{2}{x}^{2}+2x(0≤x≤2)}\\{y=\\ \frac{1}{2}{x}^{2}-4x+8(2<x≤4)}\end{array}\right.$由函数关系式可看出A中的函数图象与所求的分段函数对应.
故选:B.
点评 本题考查的动点变化过程中面积的变化关系,重点是列出函数关系式,但需注意自变量的取值范围.


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:解答题
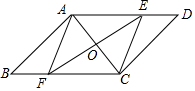 如图,在?ABCD中,对角线AC的垂直平分线EF与AC交于点O,与AD交于点E,与BC交于点F,连接EC,AF,
如图,在?ABCD中,对角线AC的垂直平分线EF与AC交于点O,与AD交于点E,与BC交于点F,连接EC,AF,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
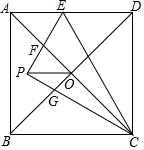 如图,在边长为4的正方形ABCD中,对角线AC,BD相交于点O,点E是AD边上一点,连接CE,把△CDE沿CE翻折,得到△CPE,EP交AC于点F,CP交BD于点G,连接PO,若PO∥BC,则四边形OFPG的面积是8-4$\sqrt{3}$.
如图,在边长为4的正方形ABCD中,对角线AC,BD相交于点O,点E是AD边上一点,连接CE,把△CDE沿CE翻折,得到△CPE,EP交AC于点F,CP交BD于点G,连接PO,若PO∥BC,则四边形OFPG的面积是8-4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
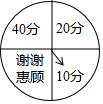 “五一”假日期间,某网店为了促销,设计了一种抽奖送积分活动,在该网店网页上显示如图所示的圆形转盘,转盘被均等的分成四份,四个扇形上分别标有“谢谢惠顾”、“10分”、“20分”、“40分”字样.参与抽奖的顾客只需用鼠标点击转盘,指针就会在转动的过程中随机的停在某个扇形区域,指针指向扇形上的积分就是顾客获得的奖励积分,凡是在活动期间下单的顾客,均可获得两次抽奖机会,求两次抽奖顾客获得的总积分不低于30分的概率.
“五一”假日期间,某网店为了促销,设计了一种抽奖送积分活动,在该网店网页上显示如图所示的圆形转盘,转盘被均等的分成四份,四个扇形上分别标有“谢谢惠顾”、“10分”、“20分”、“40分”字样.参与抽奖的顾客只需用鼠标点击转盘,指针就会在转动的过程中随机的停在某个扇形区域,指针指向扇形上的积分就是顾客获得的奖励积分,凡是在活动期间下单的顾客,均可获得两次抽奖机会,求两次抽奖顾客获得的总积分不低于30分的概率.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点D是△ABC的边AB上的一点,DE∥BC交AC于点E,作DF∥AC交BC于点F,分别记△ADE,△BDF,?DFCE,△ABC的面积为S1,S2,S3,S有以下结论:
如图,点D是△ABC的边AB上的一点,DE∥BC交AC于点E,作DF∥AC交BC于点F,分别记△ADE,△BDF,?DFCE,△ABC的面积为S1,S2,S3,S有以下结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{x-1}$ | B. | $\frac{1}{1-x}$ | C. | $\frac{5}{1-x}$ | D. | $\frac{5}{x-1}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com