
分析 首先对括号内的分式通分相减,把除法转化为乘法,计算乘法即可化简,然后确定a的值,代入计算即可.
解答 解:$\frac{{a}^{2}-2a+1}{a-2}$÷(a+2+$\frac{3}{a-2}$),
=$\frac{(a-1)^{2}}{a-2}$÷($\frac{{a}^{2}-4}{a-2}$+$\frac{3}{a-2}$)
=$\frac{(a-1)^{2}}{a-2}$÷$\frac{{a}^{2}-1}{a-2}$
=$\frac{(a-1)^{2}}{a-2}$•$\frac{a-2}{{a}^{2}-1}$
=$\frac{a-1}{a+1}$.
要使分式有意义,a≠±1且a≠2,
又因为-$\sqrt{3}$≤a≤$\sqrt{5}$,且a为整数,
所以a=0.
当a=0时,原式=$\frac{0-1}{0+1}$=-1.
点评 本题考查了分式的化简求值,分式混合运算要注意先去括号;分子、分母能因式分解的先因式分解;除法要统一为乘法运算.确定a的值是本题的关键.


科目:初中数学 来源: 题型:解答题
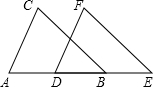 把下面的推理过程补充完整,并在括号内注明理由
把下面的推理过程补充完整,并在括号内注明理由查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某服装店专营一批进价为每件200元的品牌衬衫,每件售价为300元,每天可售出40件,若每件降价10元,则每天多售出10件,请根据以上信息解答下列问题:
某服装店专营一批进价为每件200元的品牌衬衫,每件售价为300元,每天可售出40件,若每件降价10元,则每天多售出10件,请根据以上信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
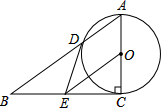 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,点E为BC的中点,连接DE.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,点E为BC的中点,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
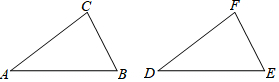
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
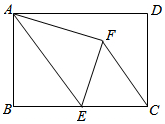 如图,在矩形ABCD中,AB=5,BC=8,点E为BC上一动点,把△ABE沿AE折叠;若点E是BC边的中点,点B落在点F处,连接CF.
如图,在矩形ABCD中,AB=5,BC=8,点E为BC上一动点,把△ABE沿AE折叠;若点E是BC边的中点,点B落在点F处,连接CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com