
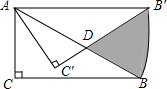
 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1,将Rt△ABC绕点A逆时针旋转30°后得到△AB′C′,则图中阴影部分的面积是
如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1,将Rt△ABC绕点A逆时针旋转30°后得到△AB′C′,则图中阴影部分的面积是| 3 |
| 3 |
| 3 |
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
| 3 |
| 3 |
| 3 |
| ||
| 3 |
| ||
| 3 |
| 3 |
| ||
| 3 |
2
| ||
| 3 |
| 30•π•22 |
| 360 |
| 1 |
| 2 |
2
| ||
| 3 |
π-
| ||
| 3 |
π-
| ||
| 3 |


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
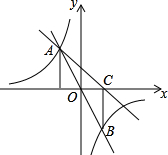 如图,在平面直角坐标系xOy中,直线y=mx与双曲线y=
如图,在平面直角坐标系xOy中,直线y=mx与双曲线y=| n |
| x |
| n |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
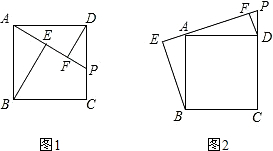
 如图,在△ABC和△DEF中,已有条件AB=DE,还需要添加两个条件才能使△ABC≌△DEF.不能添加的一组条件是( )
如图,在△ABC和△DEF中,已有条件AB=DE,还需要添加两个条件才能使△ABC≌△DEF.不能添加的一组条件是( )| A、∠B=∠E,BC=EF |
| B、∠A=∠D,BC=EF |
| C、∠A=∠D,∠B=∠E |
| D、BC=EF,AC=DF |
查看答案和解析>>
科目:初中数学 来源: 题型:
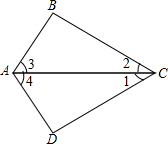 如图,AC是△ABC和△ADC的公共边,要判定△ABC≌△ADC还需要补充的条件不能是( )
如图,AC是△ABC和△ADC的公共边,要判定△ABC≌△ADC还需要补充的条件不能是( )| A、AB=AD,∠1=∠2 |
| B、AB=AD,∠3=∠4 |
| C、∠1=∠2,∠3=∠4 |
| D、∠1=∠2,∠B=∠D |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com