
【题目】如图,抛物线y=-x2+mx的对称轴为直线x=2,若关于x的-元二次方程-x2+mx-t=0 (t为实数)在l<x<3的范围内有解,则t的取值范围是( )

A.-5<t≤4 B.3<t≤4 C.-5<t<3 D.t>-5
 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 随机抛掷一枚均匀的硬币,落地后反面一定朝上。
B. 从1,2,3,4,5中随机取一个数,取得奇数的可能性较大。
C. 某彩票中奖率为![]() ,说明买100张彩票,有36张中奖。
,说明买100张彩票,有36张中奖。
D. 打开电视,中央一套正在播放新闻联播。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.“概率为0.0001的事件”是不可能事件
B.任意掷一枚质地均匀的硬币10次,正面向上的一定是5次
C.“任意画出一个等边三角形,它是轴对称图形”是随机事件
D.“任意画出一个平行四边行,它是中心对称图形”是必然事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,底边BC长为8,腰长为6,点D是BC边上一点,过点B作AC的平行线与过A、B、D三点的圆交于点E,连接DE,则DE的最小值是___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作AC的垂线交AC于点E,交AB的延长线于点F.

(1)求证:DE与⊙O相切;
(2)若CD=BF,AE=3,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
去年暑期,某地由于暴雨导致电路中断,该地供电局组织电工进行抢修.供电局距离抢修工地15千米.抢修车装载着所需材料先从供电局出发,10分钟后,电工乘吉普车从同一地点出发,结果他们同时到达抢修工地.已知吉普车速度是抢修车速度的1.5倍,求吉普车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列解题过程:
解一元二次不等式:x2-3x>0.
解:x(x-3)>0,
∴![]() 或
或![]() ,
,
解得x>3或x<0.
∴一元二次不等式x2-3x>0的解集为x<0或x>3.
结合上述解题过程回答下列问题:
(1)上述解题过程渗透的数学思想为 ;
(2)一元二次不等式x2-3x<0的解集为 ;
(3)请用类似的方法解一元二次不等式:x2-2x-3<0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC中,A(6,0)、C(0,![]() )、D(0,
)、D(0,![]() ),射线l过点D且与x轴平行,点P、Q分别是l和x轴正半轴上动点,满足∠PQO=60°.
),射线l过点D且与x轴平行,点P、Q分别是l和x轴正半轴上动点,满足∠PQO=60°.
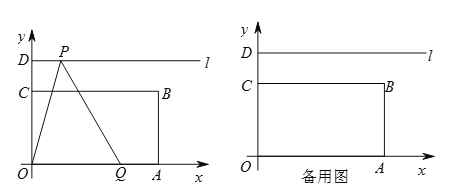
(1)①点B的坐标是 ;
②当点Q与点A重合时,点P的坐标为 ;
(2)设点P的横坐标为x,△OPQ与矩形OABC的重叠部分的面积为S,试求S与x的函数关系式及相应的自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com